题目内容
如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ.当点P运动到原点O处时,记Q的位置为B.
(1)求点B的坐标;
(2)求证:当点P在x轴上运动(P不与O重合)时,∠ABQ为定值;
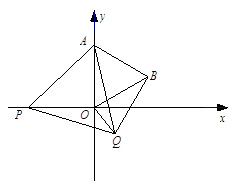
(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由.
(1)求点B的坐标;
(2)求证:当点P在x轴上运动(P不与O重合)时,∠ABQ为定值;

(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由.
解:(1)B(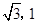 ).
).

(2)当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值90°.
(3)P的坐标为( )或(
)或(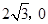 ).
).
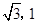 ).
). 
(2)当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值90°.
(3)P的坐标为(
 )或(
)或(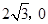 ).
).(1)因为OA=2,△AOB为等边三角形,所以B的坐标为(√3,1).
(2)因为∠PAQ和∠OAB都是60º,所以∠PAO=∠QAB,△PAQ和△OAB都是等边三角形,所以PA=QA,OA=BA,所以△PAO≌△QAB,所以∠ABQ=∠AOP=90º,所以为定值.
(3)由(2)可知,点Q总在过点B且与AB垂直的直线上,可见AO与BQ不平行.①当点P在x轴负半轴上时,点Q在点B的下方,②当点P在x轴正半轴上时,点Q在点B的上方,根据这两种情况分别求出P的坐标
(2)因为∠PAQ和∠OAB都是60º,所以∠PAO=∠QAB,△PAQ和△OAB都是等边三角形,所以PA=QA,OA=BA,所以△PAO≌△QAB,所以∠ABQ=∠AOP=90º,所以为定值.
(3)由(2)可知,点Q总在过点B且与AB垂直的直线上,可见AO与BQ不平行.①当点P在x轴负半轴上时,点Q在点B的下方,②当点P在x轴正半轴上时,点Q在点B的上方,根据这两种情况分别求出P的坐标

练习册系列答案
相关题目
 与
与
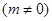 在同一坐标系内的图像可以是( )
在同一坐标系内的图像可以是( )
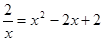 的解的个数是( )
的解的个数是( )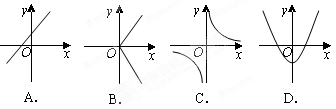


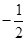 ,y1)、N(
,y1)、N(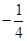 ,y2)、P(
,y2)、P(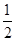 ,y3)三点都在函数
,y3)三点都在函数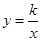 (
(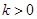 )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( )
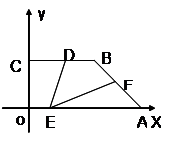
 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )