题目内容
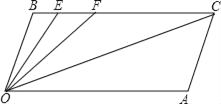
【题目】如图,CB∥OA,∠B=∠A=100°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.
(1)求∠EOC的度数;
(2)若平行移动AC,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动AC的过程中,是否存在某种情况,使∠OEB=∠OCA?若存在,求出∠OCA度数;若不存在,说明理由.
【答案】(1)40°;(2)不变,=1:2;(3)∠OCA=60°.
【解析】
(1)由于BC∥OA,∠B=100°,易求∠AOB,而OE、OC都是角平分线,从而可求∠COE;
(2)利用BC∥OA,可知∠AOC=∠BCO,又因为∠AOC=∠COF,所以就有∠FCO=∠FOC,即∠BFO=2∠FCO=2∠OCB,那么∠OCB:∠OFB=1:2;
(3)设∠OCA=α,∠AOC=x,根据三角形的外角性质、三角形的内角和定理、平行线的性质可得,α+x=80°,40°+x=α,解即可.
解:(1)∵CB∥OA,
∴∠BOA+∠B=180°,
∴∠BOA=80°,
∵∠FOC=∠AOC,OE平分∠BOF,
∴∠EOC=∠EOF+∠FOC=![]() ∠BOF+
∠BOF+![]() ∠FOA=
∠FOA=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ×80°=40°;
×80°=40°;
(2)不变.
∵CB∥OA,
∴∠OCB=∠COA,∠OFB=∠FOA,
∵∠FOC=∠AOC,
∴∠COA=![]() ∠FOA,即∠OCB:∠OFB=1:2.
∠FOA,即∠OCB:∠OFB=1:2.
(3)在平行移动AC的过程中,存在∠OEB=∠OCA,且∠OCA=60°.
设∠OCA=α,∠AOC=x,
∵∠OEB=∠COE+∠OCB=40°+x,
∠ACO=80°﹣x,
∴α=80°﹣x,40°+x=α,
∴x=20°,α=60°.

练习册系列答案
相关题目