题目内容
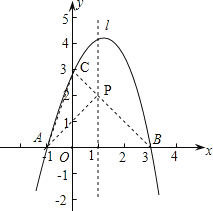
【题目】如图,已知抛物线![]() 经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.
经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.
(1)求抛物线的函数解析式及顶点D的坐标;
(2)设点P是直线上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线上是否存在点M,使△MAC为等腰三角形?若存在,求出所有符合条件的点M的坐标,若不存在,请说明理由.

【答案】(1)![]() ,D(1,4);(2)P (1,2);(3)存在,M的坐标为(1,
,D(1,4);(2)P (1,2);(3)存在,M的坐标为(1,![]() )或(1,
)或(1,![]() )或(1,1)或(1,0)
)或(1,1)或(1,0)
【解析】(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点.
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、②AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
解:(1)由抛物线y=ax2+bx+c经过A(-1,0),B(3,0),两点
∴设抛物线的解析式为y=a(x+1)(x-3),
又∵抛物线过点C(0,3), ∴3=-3a,∴a=-1,
∴y=-(x+1)(x-3),即y=-x2+2x+3,
(2)连接BC,则直线BC与直线的交点即为使△PAC的周长最小的点P.
设直线BC的解析式为y=kx+b, 将B(3,0),C(0,3)代入
得![]() , ∴
, ∴![]() ,
,
∴直线BC的函数关系式y=-x+3,
∵对称轴为直线x=1,
∴当x=1时,y=2即点P的坐标为(1,2) .
(3)由于△MAC的腰和底没有明确,因此要分三种情况讨论:
①MA=MC ②MA=AC ③AC=MC
∵抛物线的对称轴为x=1,∴设M(1,m)
∵A(-1,0),C(0,3) ∴MA2=m2+4 MC2=m2-6m+10 AC2=10
①若MA=MC 则MA2=MC2 ∴m2+4= m2-6m+10 ∴m=1,
②若MA=AC 则MA2=AC2 ∴m2+4=10,∴m=±![]()
③若MC=AC 则MC2=AC2 ∴m2-6m+10=10,∴m=0或m=6,
当m=6时,M、A、C三点共线,构不成在角形(舍去). 综上可知:存在符合条件的点M,且坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,1)或(1,0) .
)或(1,1)或(1,0) .
“点睛”熟知上述性质概念,本题综合性很强,运用的知识点很多,要认真审题才可解之,还需做辅助线求得,在二问中有两个答案易漏求,求得方法也不唯一,三问中可求有五个点,有一个不合题意需舍去,难度较大,属于难题.

