МвДїДЪИЭ
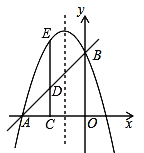
ЎѕМвДїЎїТСЦЄЦ±ПЯy=x+3Ѕ»xЦбУЪµгAЈ¬Ѕ»yЦбУЪµгBЈ¬ЕЧОпПЯy=![]() x2+bx+cѕ№эµгAЈ¬BЈ®
x2+bx+cѕ№эµгAЈ¬BЈ®
ЈЁ1Ј©ЗуЕЧОпПЯЅвОцКЅЈ»
ЈЁ2Ј©µгCЈЁmЈ¬0Ј©ФЪПЯ¶ОOAЙПЈЁµгCІ»УлAЈ¬OµгЦШєПЈ©Ј¬CDЎНOAЅ»ABУЪµгDЈ¬Ѕ»ЕЧОпПЯУЪµгEЈ¬ИфDE=![]() ADЈ¬ЗуmµДЦµЈ»
ADЈ¬ЗуmµДЦµЈ»
ЈЁ3Ј©µгMФЪЕЧОпПЯЙПЈ¬µгNФЪЕЧОпПЯµД¶ФіЖЦбЙПЈ¬ФЪЈЁ2Ј©µДМхјюПВЈ¬КЗ·сґжФЪТФµгDЈ¬BЈ¬MЈ¬NОЄ¶ҐµгµДЛД±ЯРООЄЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗлЗуіцµгNµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©y=![]() x2
x2![]() 2x+3ЈЁ2Ј©-2ЈЁ3Ј©ґжФЪЈЁ
2x+3ЈЁ2Ј©-2ЈЁ3Ј©ґжФЪЈЁ![]() 1Ј¬
1Ј¬![]() 2Ј©»тЈЁ
2Ј©»тЈЁ![]() 1Ј¬0Ј©
1Ј¬0Ј©
ЎѕЅвОцЎї·ЦОцЈєЈЁ1Ј©ПИЗуЦ±ПЯ![]() Ул
Ул![]() ЦбєН
ЦбєН![]() ЦбµДЅ»µгЧш±кЈ¬АыУГґэ¶ЁПµКэ·ЁЗуЕЧОпПЯµДЅвОцКЅЈ»
ЦбµДЅ»µгЧш±кЈ¬АыУГґэ¶ЁПµКэ·ЁЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©ёщѕЭµгCµДєбЧш±кОЄmїЙµГDєНEµДєбЧш±к¶јКЗmЈ¬ёщѕЭЅвОцКЅ±нКѕЖдЧЭЧш±кЈ¬јЖЛгЗ¦Ц±ёЯ¶ИDEµДі¤Ј¬АыУГ№ґ№Й¶ЁАнµГЈє![]() ЧоєуёщѕЭТСЦЄБРКЅїЙµГmµДЦµЈ»
ЧоєуёщѕЭТСЦЄБРКЅїЙµГmµДЦµЈ»
ЈЁ3Ј©·ЦБЅЦЦЗйїцЈє
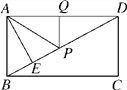
ўЩТФBCОЄТ»±ЯЈ¬ИзНј1Ј¬Ц¤Гч![]() ЎХ
ЎХ![]() Ј¬µГ
Ј¬µГ![]() їЙµГ
їЙµГ![]()
ўЪµ±BDОЄ¶ФЅЗПЯК±Ј¬ИзНј2Ј¬MФЪЕЧОпПЯµД¶ҐµгЈ¬NКЗ¶ФіЖЦбУлxЦбµДЅ»µгЈ¬ґЛК±![]()
ПкЅвЈє(1)µ±x=0К±Ј¬y=3Ј¬
ЎаB(0,3)Ј¬
µ±y=0К±Ј¬x+3=0Ј¬
x=3Ј¬
ЎаA(3,0)Ј¬
°СA(3,0),B(0,3)ґъИлЕЧОпПЯ![]() Цеãє
Цеãє
![]() ЅвµГЈє
ЅвµГЈє![]()
ЎаЕЧОпПЯµДЅвОцКЅОЄЈє![]()
(2)ЎЯCDЎНOA,C(m,0)Ј¬
Ўа![]()
Ўа![]()
ЎЯAC=m+3,CD=m+3,
УЙ№ґ№Й¶ЁАнµГЈє![]()
ЎЯ![]()
Ўа![]()
![]()
(m+3)(m+2)=0Ј¬
m1=3(Йб),m2=2Ј»
(3)ґжФЪЈ¬·ЦБЅЦЦЗйїцЈє
ўЩТФBCОЄТ»±ЯЈ¬ИзНј1Ј¬Йи¶ФіЖЦбУлxЦбЅ»УЪµгGЈ¬
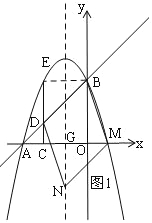
ЎЯC(2,0)Ј¬
ЎаD(2,1),E(2,3),
ЎаEУлB№ШУЪ¶ФіЖЦб¶ФіЖЈ¬
ЎаBEЎОxЦбЈ¬
ЎЯЛД±ЯРОDNMBКЗЖЅРРЛД±ЯРОЈ¬
ЎаBD=MN,BDЎОMNЈ¬
ЎЯ![]()
ЎаЎчEDBЎХЎчGNMЈ¬
ЎаNG=ED=2Ј¬
ЎаN(1,2)Ј»
ўЪµ±BDОЄ¶ФЅЗПЯК±Ј¬ИзНј2Ј¬
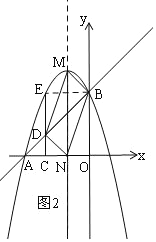
MФЪЕЧОпПЯµД¶ҐµгЈ¬NКЗ¶ФіЖЦбУлxЦбµДЅ»µгЈ¬ґЛК±ЛД±ЯРОBMDNКЗЖЅРРЛД±ЯРОЈ¬
ґЛК±N(1,0)Ј»
ЧЫЙПЛщКц,µгNµДЧш±кОЄ(1,2)»т(1,0).

 ЖЪД©ёґП°јмІвПµБРґр°ё
ЖЪД©ёґП°јмІвПµБРґр°ё і¬ДЬС§µдµҐФЄЖЪЦРЖЪД©ЧЁМвіеґМ100·ЦПµБРґр°ё
і¬ДЬС§µдµҐФЄЖЪЦРЖЪД©ЧЁМвіеґМ100·ЦПµБРґр°ё »ЖёФ360¶И¶ЁЦЖГЬѕнПµБРґр°ё
»ЖёФ360¶И¶ЁЦЖГЬѕнПµБРґр°ё Сф№вїјіЎµҐФЄІвКФѕнПµБРґр°ё
Сф№вїјіЎµҐФЄІвКФѕнПµБРґр°ё ГыРЈБЄГЛіеґМѕнПµБРґр°ё
ГыРЈБЄГЛіеґМѕнПµБРґр°ёЎѕМвДїЎїЕЧОпПЯ![]() ЙПІї·ЦµгµДєбЧш±к
ЙПІї·ЦµгµДєбЧш±к![]() Ј¬ЧЭЧш±к
Ј¬ЧЭЧш±к![]() µД¶ФУ¦ЦµИзПВ±нЈє
µД¶ФУ¦ЦµИзПВ±нЈє
x | Ў | ©Ѓ2 | ©Ѓ1 | 0 | 1 | 2 | Ў |
y | Ў | 0 | 4 | 6 | 6 | 4 | Ў |
РЎґП№ЫІмЙП±нЈ¬µГіцПВГжЅбВЫЈєўЩЕЧОпПЯУлxЦбµДТ»ёцЅ»µгОЄЈЁ3Ј¬0Ј©Ј» ўЪєЇКэ![]() µДЧоґуЦµОЄ6Ј»ўЫЕЧОпПЯµД¶ФіЖЦбКЗ
µДЧоґуЦµОЄ6Ј»ўЫЕЧОпПЯµД¶ФіЖЦбКЗ![]() Ј»ўЬФЪ¶ФіЖЦбЧуІаЈ¬yЛжxФцґу¶шФцґуЈ®ЖдЦРХэИ·УР( )
Ј»ўЬФЪ¶ФіЖЦбЧуІаЈ¬yЛжxФцґу¶шФцґуЈ®ЖдЦРХэИ·УР( )
A. ўЩўЪ B. ўЩўЫ C. ўЩўЪўЫ D. ўЩўЫўЬ