题目内容
已知:抛物线y=(k-1)x2+2kx+k-2与x轴有两个不同的交点.
(1)求k的取值范围;
(2)当k为整数,且关于x的方程3x=kx-1的解是负数时,求抛物线的解析式;
(3)在(2)的条件下,若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长?
(1)求k的取值范围;
(2)当k为整数,且关于x的方程3x=kx-1的解是负数时,求抛物线的解析式;
(3)在(2)的条件下,若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长?

(1)△=4k2-4(k-1)(k-2)=12k-8,
依题意,得
,
∴k的取值范围是k>
且k≠1,①
(2)解方程3x=kx-1,
得x=
,
∵方程3x=kx-1的解是负数,
∴3-k>0.
∴k<3,②(4分)
综合①②,可得k的取值范围是k>
且k≠1,k<3,再由k为整数,可得k=2,
∴抛物线解析式为y=x2+4x.
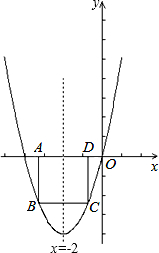
(3)如图,设最大正方形ABCD的边长为m,则B、C两点的纵坐标为-m,
且由对称性可知:B、C两点关于抛物线对称轴对称,
∵抛物线的对称轴为:x=-2,
∴点C的坐标为(-2+
,-m),
∵C点在抛物线上,
∴(-2+
)2+4(-2+
)=-m.
整理,得m2+4m-16=0,
∴m=
=-2±2
(舍负)
∴m=2
-2.
依题意,得
|
∴k的取值范围是k>
| 2 |
| 3 |
(2)解方程3x=kx-1,
得x=
| -1 |
| 3-k |
∵方程3x=kx-1的解是负数,
∴3-k>0.
∴k<3,②(4分)
综合①②,可得k的取值范围是k>
| 2 |
| 3 |
∴抛物线解析式为y=x2+4x.
(3)如图,设最大正方形ABCD的边长为m,则B、C两点的纵坐标为-m,
且由对称性可知:B、C两点关于抛物线对称轴对称,
∵抛物线的对称轴为:x=-2,
∴点C的坐标为(-2+
| m |
| 2 |
∵C点在抛物线上,
∴(-2+
| m |
| 2 |
| m |
| 2 |
整理,得m2+4m-16=0,
∴m=
-4±4
| ||
| 2 |
| 5 |
∴m=2
| 5 |


练习册系列答案
相关题目
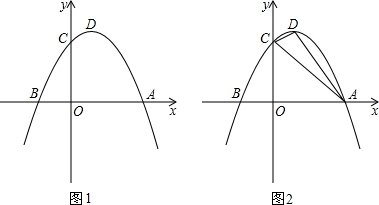
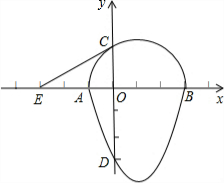

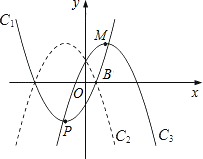 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;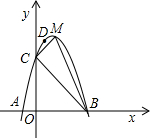 .点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.
.点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.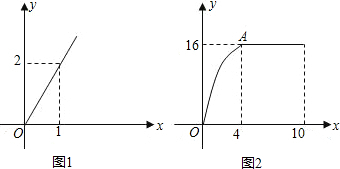 大?
大?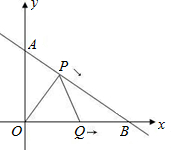 t秒(0≤t≤4)
t秒(0≤t≤4)