Question

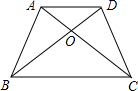如图，梯形ABCD中，AD∥BC，对角线AC、BD相交于O点，若S_△AOD：S_△OCD=1：2，则S_△AOD：S_△BOC=（　　）

• A、

  1

  6

• B、

  1

  3

• C、

  1

  4

• D、

  6

  6

Answer 1

分析：首先由于△AOD与△COD是同高的两个三角形，所以它们的面积比等于底之比，得出OA：OC=1：2，然后可证△AOD∽△COB，根据相似三角形的面积比是相似比的平方，则可得出S_△AOD：S_△BOC的值．

解答：解：设点D到AC边的距离为h，
则S_△AOD：S_△OCD=（

1

2

×OA×h）：（

1

2

×OC×h）=OA：OC=1：2．
∵AD∥BC，
∴∠DAO=∠BCO，∠ADO=∠CBO，
∴△AOD∽△COB，
∴S_△AOD：S_△BOC=（OA：OC）²=1：4．
故选C．

点评：本题主要考查了同高的两个三角形的面积比等于底之比，相似三角形的面积比是相似比的平方．