题目内容
【题目】△ABC是等边三角形,点D、E分别在AB、BC上,BD=CE,连接AE,CD交于点O
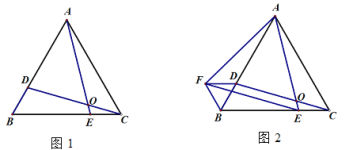
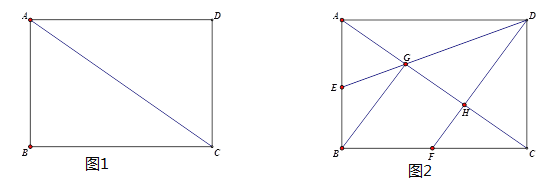
(1)如图1,求证:CD=AE;
(2)如图2,作等边△AEF,连接BF,DF.直接写出图2中所有120度的角.
【答案】(1)见解析;(2)∠ADF,∠AOC,∠DOE,∠FBC
【解析】
(1)根据等边三角形的性质得出AB=BC,∠BAC=∠ACE=∠B=60°,根据“SAS”证明△CAE≌△BCD,即可证出结论;
(2)根据等边三角形的性质直接得出120度的角即可.
解:(1)∵△ABC是等边三角形,
∴∠B=∠ACE= 60°,BC=AC.
在△BCD≌△CAE中,
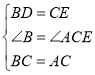 ,
,
∴△BCD≌△CAE(SAS),
∴CD=AE.
(2)∵△AEF是等边三角形,
∴∠EAF=60°,AF=AE,
∴∠FAB+∠BAE=∠CAE+∠BAE,
∴∠FAB =∠CAE.
∵AF=AE,∠FAB =∠CAE,AB=AC,
∴△AFB≌△AEC(SAS),
∴∠ABF=∠ACE=60°,FB=EC,
∴∠FBC=∠ABF+∠ABE=120°.
∵BD=CE,FB=EC,
∴BD= FB
∴∠FDB=60°,且DF∥CE,
∴∠ADF=120°.
∵ DF∥CE,且DF=CE,
∴ 四边形DFEC是平行四边形,
∴ DC∥FE
∴∠AOD=∠AEF= 60°,
∴∠AOC=120°,
∴∠DOE=∠AOC=120°.
故120度角的有∠ADF,∠AOC,∠DOE,∠FBC.

练习册系列答案
相关题目