��Ŀ����
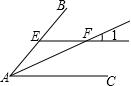
��2013•������һģ����Rt��ABC�У���ACB=90�㣬��ABC=������P�ڡ�ABC���ڲ���
��1����ͼ1��AB=2AC��PB=3����M��N�ֱ���AB��BC���ϣ���cos��=
����PMN�ܳ�����СֵΪ
��2����ͼ2��������AB=2AC���䣬��PA=
��PB=
��PC=1�����ABC�������
��3����PA=m��PB=n��PC=k����k=mcos��=nsin����ֱ��д����APB�Ķ�����

��1����ͼ1��AB=2AC��PB=3����M��N�ֱ���AB��BC���ϣ���cos��=
| ||
| 2 |
| ||
| 2 |
3
3
����2����ͼ2��������AB=2AC���䣬��PA=
| 2 |
| 10 |
��3����PA=m��PB=n��PC=k����k=mcos��=nsin����ֱ��д����APB�Ķ�����

��������1������������Ǻ�����ϵ�Լ�������Գ������·�߽����ó�����PMN���ܳ���Сֵ����P��P��ij����ֱ�������ɣ�
��2�����ȷֱ�PAB����PBC����PAC��ֱ��AB��BC��AC���ۣ���P�ĶԳƵ�ֱ��ǵ�D��E��F������DE��DF��
���PAB�ա�DAB����PCB�ա�ECB����PAC�ա�FAC�������ó���DFE=90�㣬��S�����BDAFE=2S��ABC=S��DBE+S��DFE+S��DAF��������ɣ�
��3����BM��DE��M��AN��DF��N���ֱ��ʾ����1����2����3�����ó��𰸣�
��2�����ȷֱ�PAB����PBC����PAC��ֱ��AB��BC��AC���ۣ���P�ĶԳƵ�ֱ��ǵ�D��E��F������DE��DF��
���PAB�ա�DAB����PCB�ա�ECB����PAC�ա�FAC�������ó���DFE=90�㣬��S�����BDAFE=2S��ABC=S��DBE+S��DFE+S��DAF��������ɣ�
��3����BM��DE��M��AN��DF��N���ֱ��ʾ����1����2����3�����ó��𰸣�
����⣺��1����AB=2AC��PB=3����ACB=90�㣬��ABC=����
��sin��=
��
���=30�㣬
��cos��=
��
��ͼ1����P�����AB�Լ�BC�ĶԳƵ�P�䣬P�壬
��BP=BP��=BP�䣬��PMN���ܳ���Сֵ����P��P��ij���
�ߡ�ABC=30�㣬
���P��BP��=60�㣬
���BP��P���ǵȱ������Σ�
��BP��=BP��=3��
���PMN�ܳ�����СֵΪ��3��
�ʴ�Ϊ��
��3��
��2����ͼ2���ֱ�PAB����PBC����PAC��ֱ��AB��BC��AC���ۣ���P�ĶԳƵ�ֱ��ǵ�D��E��F������DE��DF��
���PAB�ա�DAB����PCB�ա�ECB����PAC�ա�FAC��
��AD=AP=AF��BD=BP=BE��CE=CP=CF��
���ɣ�1��֪��ABC=30�㣬��BAC=60�㣬��ACB=90�㣬
���DBE=2��ABC=60�㣬��DAF=2��BAC=120�㣬
��FCE=2��ACB=180�㣮
���DBE�ǵȱ������Σ���F��C��E���ߣ�
��DE=BD=BP=
��EF=CE+CF=2CP=2��
�ߡ�ADF�У�AD=AF=
����DAF=120�㣬
���ADF=��AFD=30�㣮
��DF=
AD=
��
��EF2+DF2=10=DE2��
���DFE=90�㣮
��S�����BDAFE=2S��ABC=S��DBE+S��DFE+S��DAF��
��2S��ABC=
��(
)2+
��
��2+
��
��
=3
+
��
��S��ABC=
��
��3����APB=150�㣮
���ɣ���ͼ2����BM��DE��M��AN��DF��N��
�ɣ�2��֪��DBE=2������DAF=180��-2����
��BD=BE=n��AD=AF=m��
���DBM=������DAN=90��-����
���1=90��-������3=����
��DM=nsin����DN=mcos����
��DE=DF=EF��
���2=60�㣮
���APB=��BDA=��1+��2+��3=150�㣮
��sin��=
| 1 |
| 2 |
���=30�㣬
��cos��=
| ||
| 2 |
��ͼ1����P�����AB�Լ�BC�ĶԳƵ�P�䣬P�壬
��BP=BP��=BP�䣬��PMN���ܳ���Сֵ����P��P��ij���
�ߡ�ABC=30�㣬
���P��BP��=60�㣬
���BP��P���ǵȱ������Σ�
��BP��=BP��=3��
���PMN�ܳ�����СֵΪ��3��
�ʴ�Ϊ��
| ||
| 2 |
��2����ͼ2���ֱ�PAB����PBC����PAC��ֱ��AB��BC��AC���ۣ���P�ĶԳƵ�ֱ��ǵ�D��E��F������DE��DF��
���PAB�ա�DAB����PCB�ա�ECB����PAC�ա�FAC��
��AD=AP=AF��BD=BP=BE��CE=CP=CF��
���ɣ�1��֪��ABC=30�㣬��BAC=60�㣬��ACB=90�㣬
���DBE=2��ABC=60�㣬��DAF=2��BAC=120�㣬
��FCE=2��ACB=180�㣮
���DBE�ǵȱ������Σ���F��C��E���ߣ�
��DE=BD=BP=
| 10 |
�ߡ�ADF�У�AD=AF=
| 2 |
���ADF=��AFD=30�㣮
��DF=
| 3 |
| 6 |
��EF2+DF2=10=DE2��
���DFE=90�㣮
��S�����BDAFE=2S��ABC=S��DBE+S��DFE+S��DAF��
��2S��ABC=
| ||
| 4 |
| 10 |
| 1 |
| 2 |
| 6 |
| 1 |
| 2 |
| 6 |
| ||
| 2 |
| 3 |
| 6 |
��S��ABC=
3
| ||||
| 2 |
��3����APB=150�㣮
���ɣ���ͼ2����BM��DE��M��AN��DF��N��

�ɣ�2��֪��DBE=2������DAF=180��-2����
��BD=BE=n��AD=AF=m��
���DBM=������DAN=90��-����
���1=90��-������3=����
��DM=nsin����DN=mcos����
��DE=DF=EF��
���2=60�㣮
���APB=��BDA=��1+��2+��3=150�㣮
������������Ҫ�����˼��α任�ۺ��Լ�������Ǻ�����ϵ�Լ��ȱ������ε��ж���֪ʶ��������ԳƵó��ȱ��������ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2013•������һģ����ͼ��AF�ǡ�BAC��ƽ���ߣ�EF��AC��AB�ڵ�E������1=25�㣬���BAF�Ķ���Ϊ��������
��2013•������һģ����ͼ��AF�ǡ�BAC��ƽ���ߣ�EF��AC��AB�ڵ�E������1=25�㣬���BAF�Ķ���Ϊ�������� ��2013•������һģ����ͼ���ھ���ABCD�У�AB=2��BC=4��������ABCD�Ƶ�C��˳ʱ�뷽����ת90��õ�����FGCE����A��B��D�Ķ�Ӧ��ֱ�Ϊ��F��G��E��������P�ӵ�B��ʼ��BC-CE�˶�����E��ֹͣ������Q�ӵ�E��ʼ��EF-FG�˶�����G��ֹͣ����������˶��ٶȾ�Ϊÿ��1����λ������P�͵�Qͬʱ��ʼ�˶����˶�ʱ��Ϊx���룩����APQ�����Ϊy�����ܹ���ȷ��ӳy��x֮��ĺ�����ϵ��ͼ������ǣ�������
��2013•������һģ����ͼ���ھ���ABCD�У�AB=2��BC=4��������ABCD�Ƶ�C��˳ʱ�뷽����ת90��õ�����FGCE����A��B��D�Ķ�Ӧ��ֱ�Ϊ��F��G��E��������P�ӵ�B��ʼ��BC-CE�˶�����E��ֹͣ������Q�ӵ�E��ʼ��EF-FG�˶�����G��ֹͣ����������˶��ٶȾ�Ϊÿ��1����λ������P�͵�Qͬʱ��ʼ�˶����˶�ʱ��Ϊx���룩����APQ�����Ϊy�����ܹ���ȷ��ӳy��x֮��ĺ�����ϵ��ͼ������ǣ�������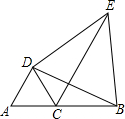 ��2013•������һģ����ͼ����C���߶�AB�ϣ���DAC�͡�DBE���ǵȱ������Σ�
��2013•������һģ����ͼ����C���߶�AB�ϣ���DAC�͡�DBE���ǵȱ������Σ�