题目内容
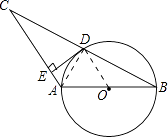
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点. 
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
【答案】
(1)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABC=30°,AB=4,
∴BD=2 ![]() ,
,
∵D是BC的中点,
∴BC=2BD=4 ![]()
(2)证明:连接OD.
∵D是BC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥AC,则∠EDO=∠CED
又∵DE⊥AC,
∴∠CED=90°,∠EDO=∠CED=90°
∴DE是⊙O的切线.
【解析】(1)根据圆周角定理求得∠ADB=90°,然后解直角三角形即可求得BD,进而求得BC即可;(2)要证明直线DE是⊙O的切线只要证明∠EDO=90°即可.
【考点精析】通过灵活运用含30度角的直角三角形和圆周角定理,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目







