题目内容
【题目】如图,在平面直角坐标系中![]() ,点
,点![]() 是
是![]() 轴正半轴上一动点,点
轴正半轴上一动点,点![]() 、
、![]() 在
在![]() 轴正半轴上.
轴正半轴上.
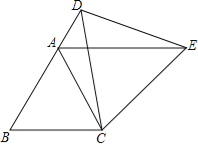
(1)如图1,若![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 的两条角平分钱,且
的两条角平分钱,且![]() 、
、![]() 交于点
交于点![]() ,直接写出
,直接写出![]() 的长度 ;
的长度 ;
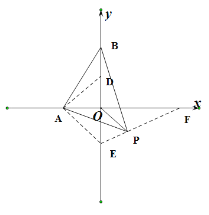
(2)如图2,![]() 是等边三角形,以线段
是等边三角形,以线段![]() 为边在第一象限内作等边
为边在第一象限内作等边![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() ,当点
,当点![]() 运动到什么位置时,满足
运动到什么位置时,满足![]() ?求点
?求点![]() 的坐标;
的坐标;
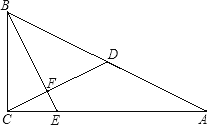
(3)如图3,以![]() 为边在
为边在![]() 的下方作等边
的下方作等边![]() ,点
,点![]() 在
在![]() 轴上运动时,求
轴上运动时,求![]() 的最小值.
的最小值.



【答案】(1)4;(2)C(8,0);(3)1
【解析】
(1)作![]() ,CH 交BD的延长线于H,分别证明
,CH 交BD的延长线于H,分别证明![]() 和
和![]() ,根据全等三角形对应边相等即可得出答案;
,根据全等三角形对应边相等即可得出答案;
(2)证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,求出CD,得出答案;
,求出CD,得出答案;
(3)以OA为对称轴作等边![]() ,连接EP,并延长EP交x轴于点F,证明点P在直线EF上运动,根据垂线段最短解答.
,连接EP,并延长EP交x轴于点F,证明点P在直线EF上运动,根据垂线段最短解答.
解:(1)作![]() ,CH 交BD的延长线于H,
,CH 交BD的延长线于H,

∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的角平分钱
的角平分钱
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
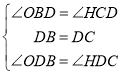
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
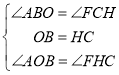
∴![]()
![]()
∴![]()
故答案为:4;
(2)∵![]() 、
、![]() 是等边三角形,
是等边三角形,
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,

∴![]()
![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴点C的坐标为:![]() ;
;
(3)以OA为对称轴作等边![]() ,连接EP,并延长EP交x轴于点F,
,连接EP,并延长EP交x轴于点F,
由(2)得,![]()
∴![]()
∴![]()
∴![]()
∴点P在直线EF上运动,当![]() 时,OP最小
时,OP最小
∴![]()
∴OP最小值为1.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】“节能环保”是对美好家园的一种守护,某汽车制造厂生产一种新型能源汽车,计划半年后每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负):
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减(辆) | +3 | -2 | -1 | +4 | +2 | -5 |
(1)生产量最多的一个月,比生产量最少的一个月多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了?多或少多少辆?