题目内容
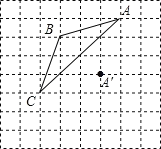
【题目】如图,直线y=kx﹣1与x轴、y轴分别交于B、C两点,且3BO﹣![]() CO=1
CO=1
(1)求点B的坐标及k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣1上的一个动点,在点A的运动过程中,试写出△AOB的面积S与x之间的函数解析式;
(3)探索:当点A运动到什么位置时,△AOB的面积是![]() ?
?

【答案】(1)k=2,B(![]() ,0);
,0);
(2)S=![]() x﹣
x﹣![]() (x>
(x>![]() );
);
(3)A点运动到(4,1)或(0,1)位置时,△AOB的面积是![]() .
.
【解析】试题分析:(1)利用坐标轴上点的坐标特征和一次函数图象上点的坐标特征先得到C(0,-1),B(![]() ,0),则利用3BO-
,0),则利用3BO-![]() CO=1得到
CO=1得到![]() -
-![]() =1,解方程得到k的值,从而得到B点坐标;(2)A点坐标表示为(x,
=1,解方程得到k的值,从而得到B点坐标;(2)A点坐标表示为(x, ![]() x-1),然后利用三角形面积公式求解;(3)设A(x,
x-1),然后利用三角形面积公式求解;(3)设A(x, ![]() x-1),利用三角形面积公式得到
x-1),利用三角形面积公式得到![]() |
|![]() x-1|=
x-1|=![]() ,然后解绝对值方程得到x的值,从而得到A点坐标.
,然后解绝对值方程得到x的值,从而得到A点坐标.
试题解析:当x=0时,y=kx﹣1=﹣1,则C(0,﹣1),
当y=0时,kx﹣1=0,解得x=![]() ,则B(
,则B(![]() ,0),
,0),
∵3BO﹣![]() CO=1
CO=1
∴![]() ﹣
﹣![]() =1,
=1,
∴k=2,
∴B(![]() ,0);
,0);
(2)y=![]() x﹣1,
x﹣1,
S=![]()
![]() (
(![]() x﹣1)
x﹣1)
=![]() x﹣
x﹣![]() (x>
(x>![]() );
);
(3)设A(x, ![]() x﹣1),
x﹣1),
∵S=![]()
![]() |
|![]() x﹣1|,
x﹣1|,
∴![]() |
|![]() x﹣1|=
x﹣1|=![]() ,解得x=4或x=0,
,解得x=4或x=0,
∴A点坐标为(4,1)或(0,1),
即A点运动到(4,1)或(0,1)位置时,△AOB的面积是![]() .
.

练习册系列答案
相关题目