题目内容
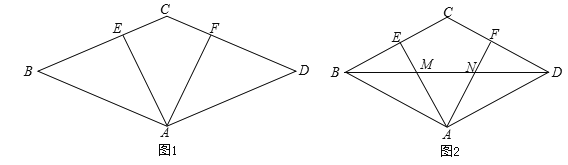
【题目】如图1,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E、F.
(1)求证:△ABE≌△ADF;
(2)若∠BAE=∠EAF,求证:AE=BE;
(3)若对角线BD与AE、AF交于点M、N,且BM=MN(如图2),求证:∠EAF=2∠BAE.
【答案】解:(1)∵菱形ABCD,
∴AB=AD,∠ABE =∠ADF,————————————(2分)
又∵AE⊥BC,AF⊥CD,
∴∠AEB =∠AFD,————————————————(1分)
∴△ABE≌△ADF. ————————————————(1分)
(2)∵菱形ABCD,
∴AB‖CD,
又∵AF⊥CD,
∴AF⊥AB,
∴∠BAF=![]() ,又∠BAE=∠EAF,
,又∠BAE=∠EAF,
∴∠BAE=![]() ,∠AEB=
,∠AEB=![]() ,———————————(2分)
,———————————(2分)
∴∠B=![]() =∠BAE,———————————————(1分)
=∠BAE,———————————————(1分)
∴AE="BE." ———————————————————(1分)
(3) ∵△ABE≌△ADF,
∴∠BAE =∠DAF,AB=AD,
∴∠ABM =∠ADN,
∴△ABM≌△ADN.
∴AM =AN,———————————————————(1分)
又∵∠BAN=![]() , BM=MN,
, BM=MN,
∴AM=MN=AN,
∴∠MAN=![]() ,——————————————————(1分)
,——————————————————(1分)
∴∠MAB=![]() ,——————————————————(1分)
,——————————————————(1分)
∴∠EAF=2∠BAE. ————————————————(1分)
【解析】略

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
