题目内容
【题目】下面从认知、延伸、应用三个层面来研究一种几何模型.
(认知)
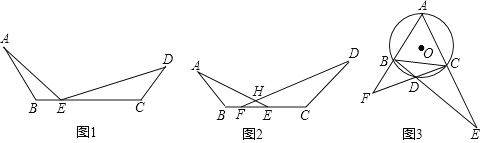
如图1,已知点E是线段BC上一点,若![]() 求证:
求证:![]() ∽
∽![]() .
.
(延伸)
如图2,已知点E、F是线段BC上两点,AE与DF交于点H,若![]() 求证:
求证:![]() ∽
∽![]() .
.
(应用)
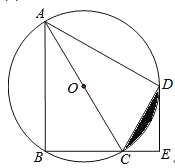
如图3,![]() 是等边
是等边![]() 的外接圆,点D是
的外接圆,点D是![]() 上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点
上一点,连接BD并延长交AC的延长线于点E;连接CD并延长交AB的延长线于点![]() 猜想BF、BC、CE三线段的关系,并说明理由.
猜想BF、BC、CE三线段的关系,并说明理由.
【答案】【认知】:详见解析;【延伸】:详见解析;【应用】:![]() ,证明详见解析.
,证明详见解析.
【解析】
认知:由∠AEC=∠A+∠B=∠AED+∠DEC,结合∠B=∠AED知∠A=∠DEC,再由∠B=∠C即可得证;延伸:由∠HFE+∠FHE=∠A+∠B,由∠B=∠AHD=∠FHE知∠A=∠HFE,再由∠B=∠C即可得证△ABE∽△FCD;应用:由∠BDC+∠A=180°及∠A=60°知∠BDC=∠FDE=120°,由∠ABC=∠ACB=60°知∠FBC=∠ECB=∠FDE=120°,与“延伸”解答过程同理可证△FBC∽△BCE得![]() ,,从而得出答案.
,,从而得出答案.
解:【认知】
证明:![]() 是
是![]() 的外角,
的外角,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ∽
∽![]() .
.
【延伸】
证明:![]() 是
是![]() 的外角,
的外角,
![]() ,
,
![]() 是
是![]() 的外角,
的外角,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() .
.
【应用】
猜想:![]() ,
,
证明:![]() 四边形ABDC是
四边形ABDC是![]() 的内接四边形,
的内接四边形,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的外角,
的外角,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |

【题目】二次函数y=2x2﹣8x+m满足以下条件:当﹣2<x<﹣1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为( )
A. 8 B. ﹣10 C. ﹣42 D. ﹣24
【题目】在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )
A. m>n B. m<n C. m=n D. 无法确定