题目内容
如图,直线y=ax(a>0)与双曲线交于A,B两点,且点A的坐标为(4,m),点B的坐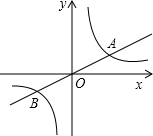 标为(n,-2)
标为(n,-2)(1)求m、n的值;
(2)若双曲线y=
| k |
| x |
(3)过原点O的另一条直线l交双曲线y=
| k |
| x |
分析:由双曲线的对称性知m=2,n=-4;由条件(1)知,k=8,点C的纵坐标为8,横坐标就为1,进而求出CO的长,可求出△MOC的面积;可求△AOC的面积.
解答: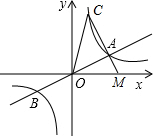 解:(1)由双曲线的对称性知m=2,n=-4;
解:(1)由双曲线的对称性知m=2,n=-4;
(2)∵k=8,点C的纵坐标为8,
∴C点横坐标为:1,
∴设直线CA的解析式为:y=kx+b,
∴将A(4,2),C(1,8)代入得:
,
解得:
,
y=-2x+10,
∴M点坐标为:(5,0),
∴△AOC的面积为:S△COM-S△AOM=
×8×5-
×2×5=15;
(3)△AOP的面积为6.
 解:(1)由双曲线的对称性知m=2,n=-4;
解:(1)由双曲线的对称性知m=2,n=-4;(2)∵k=8,点C的纵坐标为8,
∴C点横坐标为:1,
∴设直线CA的解析式为:y=kx+b,
∴将A(4,2),C(1,8)代入得:
|
解得:
|
y=-2x+10,
∴M点坐标为:(5,0),
∴△AOC的面积为:S△COM-S△AOM=
| 1 |
| 2 |
| 1 |
| 2 |
(3)△AOP的面积为6.
点评:本题考查反比例函数图象性质求面积关键知道点到直线的距离公式.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 11、如图,直线y=ax+b经过点(-4,0),则不等式ax+b≥0的解集为
11、如图,直线y=ax+b经过点(-4,0),则不等式ax+b≥0的解集为 >0)相交于点P,PC⊥x轴于点C,点A的坐标为(-4,0),点B的坐标为(0,2),PC=3.
>0)相交于点P,PC⊥x轴于点C,点A的坐标为(-4,0),点B的坐标为(0,2),PC=3. (2013•大连一模)如图.直线y=ax+b与双曲线
(2013•大连一模)如图.直线y=ax+b与双曲线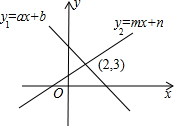 如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )
如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )