题目内容
 (2013•大连一模)如图.直线y=ax+b与双曲线y=
(2013•大连一模)如图.直线y=ax+b与双曲线y=| k |
| x |
(1)求直线与双曲线的解析式;
(2)求不等式ax+b>
| k |
| x |
分析:(1)先把先把(1,2)代入双曲线y=
中,可求k,从而可得双曲线的解析式,再把y=-4代入双曲线的解析式中,可求m,最后把(1,2)、(-
,-4)代入一次函数,可得关于a、b的二元一次方程组,解可求a、b的值,进而可求出一次函数解析式;
(2)根据图象观察可得x>1或-
<x<0.主要是观察交点的左右即可.
| k |
| x |
| 1 |
| 2 |
(2)根据图象观察可得x>1或-
| 1 |
| 2 |
解答: 解:(1)先把(1,2)代入双曲线y=
解:(1)先把(1,2)代入双曲线y=
中,得
k=2,
∴双曲线的解析式是y=
,
当y=-4时,m=-
,
把(1,2)、(-
,-4)代入一次函数,可得
,
解得
,
∴一次函数的解析式是y=4x-2;
(2)根据图象可知,若ax+b>
,那么x>1或-
<x<0.
 解:(1)先把(1,2)代入双曲线y=
解:(1)先把(1,2)代入双曲线y=| k |
| x |
k=2,
∴双曲线的解析式是y=
| 2 |
| x |
当y=-4时,m=-
| 1 |
| 2 |
把(1,2)、(-
| 1 |
| 2 |
|
解得
|
∴一次函数的解析式是y=4x-2;
(2)根据图象可知,若ax+b>
| k |
| x |
| 1 |
| 2 |
点评:本题考查了一次函数与反比例函数交点问题,解题的关键是掌握待定系数法求函数解析式,并会根据图象求出不等式的解集.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
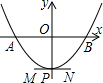 (2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
(2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( ) (2013•大连一模)如图是由四个完全相同的正方体组成的几何体,这个几何体的俯视图是( )
(2013•大连一模)如图是由四个完全相同的正方体组成的几何体,这个几何体的俯视图是( )