题目内容
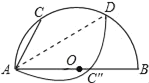
【题目】如图,半圆的直径AB=10cm,弦AC=6cm,把AC沿直线AD对折恰好与AB重合,则AD的长为( )
A.4![]() cmB.3
cmB.3![]() cmC.5
cmC.5![]() cmD.8cm
cmD.8cm
【答案】A
【解析】
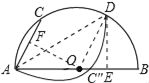
设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F,运用圆周角定理,可证得∠DOB=∠OAC,即证△AOF≌△OED,所以OE=AF=3cm,根据勾股定理,得DE=4cm,在直角三角形ADE中,根据勾股定理,可求AD的长.
设圆的圆心是O,连接OD,AD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∠CAD=∠BAD,
∴![]() ,
,
∴点D是弧BC的中点.
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△OED,
∴OE=AF=3cm,
∴DE=4cm,
∴AD=![]() =4
=4![]() cm.
cm.
故选:A.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目