题目内容
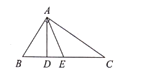
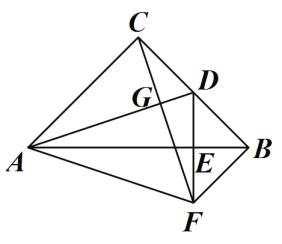
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,有下列条件:
上,有下列条件:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,能使四边形
.其中,能使四边形![]() 是平行四边形的条件有( ).
是平行四边形的条件有( ).

A.1个B.2个C.3个D.4个
【答案】C
【解析】
在ABCD中,AD=BC,AD∥BC,又BE=DF,得出AF=EC,即可得出四边形AECF是平行四边形,①正确;由AF∥EC,AE∥CF,得出四边形AECF是平行四边形,②正确;由平行四边形的性质和∠BAE=∠DCF证出AE∥CF,得出四边形AECF是平行四边形,④正确;③不正确;即可得出结果.
①正确,理由如下:
∵四边形ABCD平行四边形,
∴AD=BC,AD∥BC,
又∵BE=DF,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
②正确,理由如下:
∵AF∥EC,AE∥CF,
∴四边形AECF是平行四边形;
④正确;理由如下:
∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠BAE=∠DCF,
∴∠AEB=∠CFD.
∵AD∥BC,
∴∠AEB=∠EAD.
∴∠CFD=∠EAD.
∴AE∥CF.
∵AF∥CE,
∴四边形AECF是平行四边形.
∵AE=CF不能得出四边形AECF是平行四边形,
∴③不正确;
能使四边形AECF是平行四边形的条件有3个.
故选:C.

练习册系列答案
相关题目