��Ŀ����
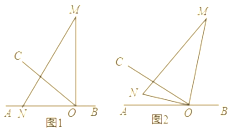
����Ŀ����ͼ,OΪֱ��AB��һ��,����O������OC,��AOC=30��,��һֱ�����ǰ� (��M=30��)��ֱ�Ƕ�����ڵ�O��,һ��ON������OA��,��һ��OM��OC����ֱ��AB���Ϸ�,����ͼ�е����ǰ��Ƶ�O��ÿ��3����ٶ���˳ʱ�뷽����תһ�ܡ�
(1)�����ON��OC�غ�?
(2)��ͼ������t���MN��AB�����ʱt��ֵ��
(3)�����ǰ���ת����ͬʱ,����OCҲ��O����ÿ��6����ٶ���˳ʱ�뷽����תһ�ܣ���ô�����ʱ��OC��OM�غ�?�뻭ͼ��˵�����ɡ�
��4���ڣ�3���������£����ʱ��OCƽ�֡�MOB?�뻭ͼ��˵�����ɡ�
���𰸡���1��10���ON��OC�غϣ���2������t=20���MN��AB����3��t=20�룬����������4��t=![]() �룬������.
�룬������.
��������
��1���ýǵĶ�������ת���ٶȼ��ɵã�
��2������MN��AB���ɵá�BOM����M��30��������֪��ת�Ķ����������ת�ٶȿɵ�ʱ��t��
��3������OC��OM�غϵá�BOC=��BOM�������ת�ٶȿɵá�AON=3t,��AOC=30+6t�������ڲ��ǵĶ�����ʽ�������t��ֵ���ɣ�
��4������ת���ٶȹ�ϵ��OCƽ�֡�MOB��ͼ���ɣ�
�⣺ (1)��30��3=10��
��10���ON��OC�غϣ�
(2) ��MN��AB
���BOM����M��30��
�ߡ�AON +��BOM=90����
���AON��60����
��t=60��3=20
�ྭ��20���MN��AB��
��3����ͼ��

�ߡ�AON+��BOM=90����BOC=��BOM��
�����ǰ��Ƶ�O��ÿ��3�����ٶ�,
����OCҲ��O����ÿ��6�����ٶ���ת��
���AON=3t,��AOC=30��+6t��
��OC��OM�غ�
�ߡ�AOC+��BOC=180��
�ɵã���30��+6t��+��90��3t����180��
��ã�t=20�� ��
(4)��ͼ��
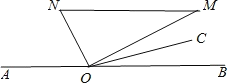
�ߡ�AON+��BOM=90������BOC=��COM��
�����ǰ��Ƶ�O��ÿ��3�����ٶ�,
����OCҲ��O����ÿ��6�����ٶ���ת��
���AON=3t,��AOC=30��+6t��
���BOC=��COM=![]() (90��3t)��
(90��3t)��
�ߡ�BOM+��AON=90����
�ɵã�180��(30��+6t)=![]() (90��3t)��
(90��3t)��
��ã�t=![]() ��.
��.
�ʴ�Ϊ����1��10���ON��OC�غϣ���2������t=20���MN��AB����3��t=20�룬����������4��t=![]() �룬������.
�룬������.

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�