Question

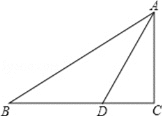
【题目】已知：如图，在 Rt△ABC 中，∠C＝90°，∠B＝30°，AD 平分∠BAC．

（1）求证：点 D 在 AB 的垂直平分线上；

（2）若 CD=2，求 BC 的长．

Answer 1

【答案】（1）证明见解析；（2）6

【解析】

（1）先根据三角形内角和定理得∠BAC＝60°，再根据AD 平分∠BAC，可得∠BAD＝∠B＝30°，即AD＝BD，得证点D在AB的垂直平分线上；

（2）根据特殊三角函数值求得AD＝2CD=4，结合（1）得BD＝AD=4，即可求出BC 的长．

（1）在Rt△ABC中，∠C＝90°，∠B＝30°，

∴∠BAC＝60°．

又∵AD平分∠BAC，

∠BAD＝∠CAD＝30°

∴∠BAD＝∠B＝30°，

∴AD＝BD

∴点D在AB的垂直平分线上

（2）∵AD＝BD，∠B＝30°

∴

∴

在Rt△ACD中，∠C＝90°，

∴AD＝2CD=4

由（1）得BD＝AD=4

∴BC＝BD+CD=2+4=6