题目内容
如图BC⊥ED于点M,∠A=27°,∠D=20°,则∠B= °,∠ACB= °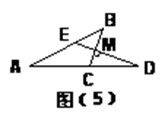

43° 110°
根据三角形内角和外角的关系解答.
解:∵在△AED中,∠A=27°,∠D=20°,
∴∠BED=∠A+∠D=27°+20°=47°,
又∵BC⊥ED于点M,
∴∠B=90°-47°=43°,
∠ACB=∠D+∠CMD=20°+90°=110°.
解:∵在△AED中,∠A=27°,∠D=20°,
∴∠BED=∠A+∠D=27°+20°=47°,
又∵BC⊥ED于点M,
∴∠B=90°-47°=43°,
∠ACB=∠D+∠CMD=20°+90°=110°.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

 )点E是线段AD的中点吗?说
)点E是线段AD的中点吗?说 明理由;
明理由; =
=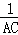 +
+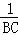 ;③MN≤
;③MN≤ AB,其中正确结论的个数是( )
AB,其中正确结论的个数是( )