题目内容
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形:
(1)使三角形的三边长分别为![]() (在图1中画一个即可);
(在图1中画一个即可);
(2)使三角形为钝角三角形且面积为4(在图2中画一个即可)。
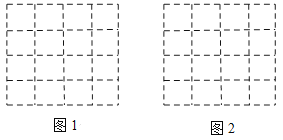
【答案】(1)![]() (2)
(2)
【解析】
试题分析:(1)先在正方形网格中取线段长为整数的线段BC=3,然后根据勾股定理找出点A的位置;
(2)先在正方形网格中取EF=2;然后由三角形的面积公式入手求得EF边上的高线的长度;最后根据钝角三角形的定义确定点D的位置.
试题解析:(1)如图1所示,BC=3,AB=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ;
;
(2)如图2所示:根据三角形的面积公式知,![]() ×EF×hD=4,即
×EF×hD=4,即![]() ×2×hD=4,
×2×hD=4,
解得hD=4.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 ,中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.