题目内容
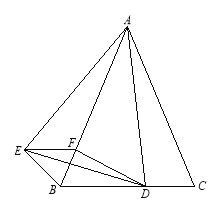
【题目】已知AM是△ABC的中线,点D在线段AM上[点D不与点A重合),过点D作DF∥AB交AC边于点F,过点C作CE∥AM交DF的延长线于点E,连接AE.
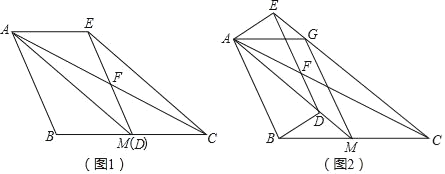
(1)如图1,当点D与点M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与点M重合时,过点M作MG∥DE交EC于点G,连接BD、AG在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形.
【答案】(1)见解析;(2)图中所有的平行四边形为平行四边形ABMG,平行四边形AMCG,平行四边形DEGM,平行四边形ABDE.
【解析】
(1)由平行线的性质得出∠EDC=∠ABD,∠ECD=∠ADB,由中线性质得出BD=DC,证明△ABD≌△EDC,得出AB=ED,即可得出结论;
(2)同(1)得:四边形ABMG是平行四边形,得出AG∥BC,AB=MG,由CE∥AM,得出四边形AMCG是平行四边形,由MG∥DE,CE∥AM,得出四边形DEGM是平行四边形,得出DE=MG,证出AB=DE,即可得出四边形ABDE是平行四边形.
解:(1)证明:∵DF∥AB,CE∥AM,
∴∠EDC=∠ABD,∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
在△ABD和△EDC中,

∴△ABD≌△EDC(ASA),
∴AB=ED,
∵AB∥ED,
∴四边形ABDE是平行四边形;
(2)图中所有的平行四边形为平行四边形ABMG,平行四边形AMCG,平行四边形DEGM,平行四边形ABDE;理由如下:
同(1)得:四边形ABMG是平行四边形,
∴AG∥BC,AB=MG,
∵CE∥AM,
∴四边形AMCG是平行四边形,
∵MG∥DE,CE∥AM,
∴四边形DEGM是平行四边形,
∴DE=MG,
∴AB=DE,
又∵DF∥AB,
∴四边形ABDE是平行四边形.