ћвƒњƒЏ»Ё
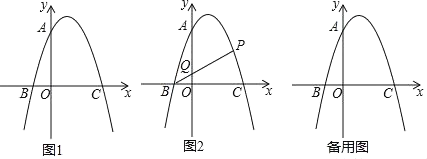
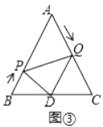
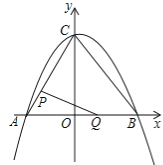
°Њћвƒњ°њ»зЌЉҐў£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђґюіќЇѓ эy£љ![]() x2+bx+cµƒЌЉѕу”л„ш±к÷бљї”ЏA£ђB£ђC»эµг£ђ∆д÷–µгAµƒ„ш±кќ™£®©Б3£ђ0£©£ђµгBµƒ„ш±кќ™£®4£ђ0£©£ђЅђљ”AC£ђBC£ЃґѓµгPі”µгA≥цЈҐ£ђ‘ЏѕяґќAC…ѕ“‘√њ√л1Єцµ•ќї≥§ґ»µƒЋўґ»ѕтµгC„ч‘»Ћў‘Ћґѓ£їЌђ ±£ђґѓµгQі”µгO≥цЈҐ£ђ‘ЏѕяґќOB…ѕ“‘√њ√л1Єцµ•ќї≥§ґ»µƒЋўґ»ѕтµгB„ч‘»Ћў‘Ћґѓ£ђµ±∆д÷–“їµгµљіп÷’µг ±£ђЅн“їµгЋж÷ЃЌ£÷є‘Ћґѓ£ђ…и‘Ћґѓ ±Љдќ™t√л£ЃЅђљ”PQ£Ѓ
x2+bx+cµƒЌЉѕу”л„ш±к÷бљї”ЏA£ђB£ђC»эµг£ђ∆д÷–µгAµƒ„ш±кќ™£®©Б3£ђ0£©£ђµгBµƒ„ш±кќ™£®4£ђ0£©£ђЅђљ”AC£ђBC£ЃґѓµгPі”µгA≥цЈҐ£ђ‘ЏѕяґќAC…ѕ“‘√њ√л1Єцµ•ќї≥§ґ»µƒЋўґ»ѕтµгC„ч‘»Ћў‘Ћґѓ£їЌђ ±£ђґѓµгQі”µгO≥цЈҐ£ђ‘ЏѕяґќOB…ѕ“‘√њ√л1Єцµ•ќї≥§ґ»µƒЋўґ»ѕтµгB„ч‘»Ћў‘Ћґѓ£ђµ±∆д÷–“їµгµљіп÷’µг ±£ђЅн“їµгЋж÷ЃЌ£÷є‘Ћґѓ£ђ…и‘Ћґѓ ±Љдќ™t√л£ЃЅђљ”PQ£Ѓ
£®1£©ћоњ’£Їb£љ £ђc£љ £ї
£®2£©‘ЏµгP£ђQ‘Ћґѓєэ≥ћ÷–£ђ°чAPQњ…ƒ№ «÷±љ«»эљ«–ќ¬р£њ«лЋµ√чјн”…£ї
£®3£©µгM‘Џ≈„ќпѕя…ѕ£ђ«“°чAOMµƒ√жїэ”л°чAOCµƒ√жїэѕаµ»£ђ«у≥цµгMµƒ„ш±к°£
°Њір∞Є°њ£®1£©![]() £ђ4£ї£®2£©≤їњ…ƒ№ «÷±љ«»эљ«–ќ£ђЉыљвќц£ї£®3£©M(1,4)їтM(
£ђ4£ї£®2£©≤їњ…ƒ№ «÷±љ«»эљ«–ќ£ђЉыљвќц£ї£®3£©M(1,4)їтM(![]() ,-4£©їтM(
,-4£©їтM(![]() ,-4£©
,-4£©
°Њљвќц°њ
(1)…и≈„ќпѕяµƒљвќц љќ™y=a£®x+3£©£®x-4£©£ЃљЂa=-![]() іъ»лњ…µ√µљ≈„ќпѕяµƒљвќц љ£ђі”ґшњ…»Јґ®≥цb°Ґcµƒ÷µ£ї
іъ»лњ…µ√µљ≈„ќпѕяµƒљвќц љ£ђі”ґшњ…»Јґ®≥цb°Ґcµƒ÷µ£ї
£®2£©ѕ»«уµ√µгCµƒ„ш±к£ђ“јЊЁєіє…ґ®јнњ…«уµ√AC=5£ђ‘тPC=5-t£ђAQ=3+t,‘ў≈–ґѕµ±°чAPQ «÷±љ«»эљ«–ќ ±£ђ‘т°ѕAPQ£љ90°г£ђі”ґшµ√≥ц![]() AOC
AOC![]() APQ£ђµ√µљ±»јэ љЅ–Јљ≥ћ«уљвЉіњ…£ї
APQ£ђµ√µљ±»јэ љЅ–Јљ≥ћ«уљвЉіњ…£ї
(3)ЄщЊЁµгM‘Џ≈„ќпѕя…ѕ£ђ…и≥цµгMµƒ„ш±кќ™£®m£ђ©Б![]() m2+
m2+![]() m+4£©£ђ‘ўЄщЊЁ°чAOMµƒ√жїэ”л°чAOCµƒ√жїэѕаµ»£ђі”ґшµ√≥ц©Б
m+4£©£ђ‘ўЄщЊЁ°чAOMµƒ√жїэ”л°чAOCµƒ√жїэѕаµ»£ђі”ґшµ√≥ц©Б![]() m2+
m2+![]() m+4=
m+4=![]() £ђљвЈљ≥ћЉіњ…£Ѓ
£ђљвЈљ≥ћЉіњ…£Ѓ
љв£Ї£®1£©…и≈„ќпѕяµƒљвќц љќ™y£љa£®x+3£©£®x©Б4£©£ЃљЂa£љ©Б![]() іъ»лµ√£Їy£љ©Б
іъ»лµ√£Їy£љ©Б![]() x2+
x2+![]() x+4£ђ
x+4£ђ
°аb£љ![]() £ђc£љ4£Ѓ
£ђc£љ4£Ѓ
£®2£©‘ЏµгP°ҐQ‘Ћґѓєэ≥ћ÷–£ђ°чAPQ≤їњ…ƒ№ «÷±љ«»эљ«–ќ£Ѓ
јн”…»зѕ¬£Ї°я‘ЏµгP°ҐQ‘Ћґѓєэ≥ћ÷–£ђ°ѕPAQ°Ґ°ѕPQA Љ÷’ќ™»сљ«£ђ
°аµ±°чAPQ «÷±љ«»эљ«–ќ ±£ђ‘т°ѕAPQ£љ90°г£Ѓ
љЂx£љ0іъ»л≈„ќпѕяµƒљвќц љµ√£Їy£љ4£ђ
°аC£®0£ђ4£©£Ѓ°яµгAµƒ„ш±кќ™£®©Б3£ђ0£©£ђ
°а‘ЏRt°чAOC÷–£ђ“јЊЁєіє…ґ®јнµ√£ЇAC£љ5£ђ
°яAP£љOQ£љt£ђ°аAQ=3+t£ђ
°я°ѕOAC£љ°ѕPAQ£ђ°ѕAPQ£љ°ѕAOC
°а![]() AOC
AOC![]() APQ
APQ
°аAP:AO=AQ:AC
°а![]() =
=![]() °аt=4.5£Ѓ
°аt=4.5£Ѓ
°я”…ћв“вњ…÷™£Ї0°№t°№4£ђ
°аt£љ4.5≤їЇѕћв“в£ђЉі°чAPQ≤їњ…ƒ№ «÷±љ«»эљ«–ќ£Ѓ
(3 )…иµгMµƒ„ш±кќ™£®m£ђ©Б![]() m2+
m2+![]() m+4£©
m+4£©
°я°чAOMµƒ√жїэ”л°чAOCµƒ√жїэѕаµ»£ђ«“µ„ґЉќ™AO£ђC£®0£ђ4£©£Ѓ
°а©Б![]() m2+
m2+![]() m+4=
m+4=![]()
µ±©Б![]() m2+
m2+![]() m+4=-4 ±£ђљвµ√£Їm=
m+4=-4 ±£ђљвµ√£Їm=![]() їт
їт![]() ,
,
µ±©Б![]() m2+
m2+![]() m+4=4 ±£ђљвµ√£Їm=1їт0
m+4=4 ±£ђљвµ√£Їm=1їт0
°яµ±m=0 ±£ђ”лC÷ЎЇѕ£ђ°аm=![]() їт
їт![]() їт1
їт1
°а M(1,4)їтM(![]() ,-4£©їтM(
,-4£©їтM(![]() ,-4£©
,-4£©

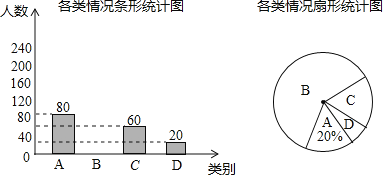
°Њћвƒњ°њƒ≥±цєЁ”–»фЄ…Љд±к„ЉЈњ£ђµ±±к„ЉЈњµƒЉџЄсќ™![]() ‘™ ±£ђ√њћм»л„°µƒєъЉд эќ™
‘™ ±£ђ√њћм»л„°µƒєъЉд эќ™![]() Љд£ђЊ≠ –≥°µч≤й±н√ч£ђЄ√±цєЁ√њЉд±к„ЉЈњµƒЉџЄс‘Џ
Љд£ђЊ≠ –≥°µч≤й±н√ч£ђЄ√±цєЁ√њЉд±к„ЉЈњµƒЉџЄс‘Џ![]() ‘™÷ЃЉд£®Їђ
‘™÷ЃЉд£®Їђ![]() ‘™£ђ
‘™£ђ![]() ‘™£©Є°ґѓ ±£ђ√њћм»Ћ„°µƒЈњЉд э
‘™£©Є°ґѓ ±£ђ√њћм»Ћ„°µƒЈњЉд э![]() £®Љд£©”л√њЉд±к„ЉЈњµƒЉџЄс
£®Љд£©”л√њЉд±к„ЉЈњµƒЉџЄс![]() £®‘™£©µƒ эЊЁ»зѕ¬±н£Ї
£®‘™£©µƒ эЊЁ»зѕ¬±н£Ї
| °≠°≠ | 190 | 200 | 210 | 220 | °≠°≠ |
| °≠°≠ | 65 | 60 | 55 | 50 | °≠°≠ |
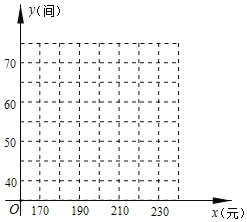
£®1£©ЄщЊЁЋщЄш эЊЁ‘Џ„ш±кѕµ÷–√и≥цѕа”¶µƒµг£ђ≤Ґї≠≥цЌЉѕу£Ѓ
£®2£©≤¬ѕл£®1£©÷–µƒЌЉѕу « ≤√іЇѓ эµƒЌЉѕу£ђ«у![]() єЎ”Џ
єЎ”Џ![]() µƒЇѓ э±ніп љ£ђ≤Ґ–і≥ц„‘±дЅњ
µƒЇѓ э±ніп љ£ђ≤Ґ–і≥ц„‘±дЅњ![]() µƒ»°÷µЈґќІ£Ѓ
µƒ»°÷µЈґќІ£Ѓ
£®3£©…ињЌЈњµƒ»’”™“µґоќ™W (‘™)£Ѓ»ф≤їњЉ¬«∆дЋы“тЋЎ£ђќ ±цєЁ±к„ЉЈњµƒЉџЄсґ®ќ™ґа…ў‘™ ±£ђњЌЈњµƒ»’”™“µґо„оіу£њ„оіуќ™ґа…ў‘™£њ