题目内容
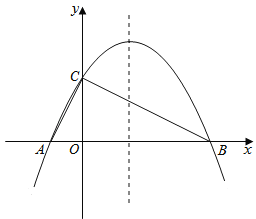
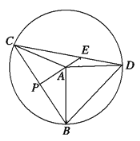
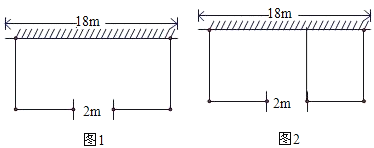
【题目】如图1，若要建一个长方形鸡场，鸡场的一边靠墙（墙长18米），墙对面有一个2米宽的门，另三边用竹篱笆围成，篱笆总长33米．
求：（1）若鸡场面积150平方米，鸡场的长和宽各为多少米？
（2）鸡场面积可能达到200平方米吗？
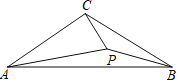
（3）如图2，若在鸡场内要用竹篱笆加建一道隔栏，则鸡场最大面积可达多少平方米？
【答案】（1）长为15米，宽为10米；（2）不可能达到200平方米；（3）
【解析】
（1）若鸡场面积150平方米，求鸡场的长和宽，关键是用一个未知数表示出长或宽，并注意去掉门的宽度；
（2）求二次函数的最值问题，列出面积的关系式化为顶点式，确定函数最大值与200的大小关系，即可得到答案；
（3）此题中首先设出鸡场的面积和宽，列函数式时要注意墙宽有三条道，所以鸡场的长要用篱笆的周长减去3个宽再加上大门的宽2米，再求函数式的最大值．
（1）设宽为x米，则：x（33﹣2x+2）＝150，
解得：x1＝10，x2＝
（不合题意舍去），
∴长为15米，宽为10米；
（2）设面积为w平方米，则：W＝x（33﹣2x+2），
变形为： 
，
∴鸡场面积最大值为
=153
＜200，即不可能达到200平方米；
（3）设此时面积为Q平方米，宽为x米，则：Q＝x（33﹣3x+2），
变形得：Q＝﹣3（x-
）2+ ，
∴此时鸡场面积最大值为．
【题目】超市有
，
两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买型瓶3个或以上，一次性返还现金5元，设购买型瓶
（个），所需总费用为
（元），则下列说法不一定成立的是（ ）
型号 | A | B |
单个盒子容量（升） | 2 | 3 |
单价（元） | 5 | 6 |
A.购买型瓶的个数是
为正整数时的值B.购买型瓶最多为6个
C.与之间的函数关系式为
D.小张买瓶子的最少费用是28元
