��Ŀ����
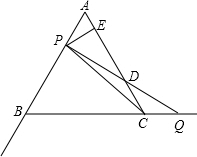 ��ABC�DZ߳�Ϊ4�ĵȱ������Σ�������AB��BC�Ϸֱ��ж���P��Q����AP=CQ������PQ��ֱ��AC�ڵ�D����PE��AC������ΪE��
��ABC�DZ߳�Ϊ4�ĵȱ������Σ�������AB��BC�Ϸֱ��ж���P��Q����AP=CQ������PQ��ֱ��AC�ڵ�D����PE��AC������ΪE����1����ͼ������P�ڱ�AB�����A��B���غϣ��ϣ��ʣ�
���߶�PD���߶�DQ֮���������Ĵ�С��ϵ����֤����Ľ��ۣ�
�����ŵ�P��Q���ƶ����߶�DE�ij��ܷ�ȷ�������ܣ����DE�ij��������ܣ���Ҫ˵�����ɣ�
��2������P������AB�ϣ�����AP=x��CD=y����
��y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
�ڵ�xΪ��ֵʱ����PCQ��������ABC�������ȣ�
��������1������PG��BC��AC��G��DH��AB��BQ��H���Ƴ���DHC����APGΪ�ȱ������θ���������ȫ�ȣ����DP=DQ���ڸ���AE=EG��GD=DC���������DE=
AC��
��2����Ϊ������������ǣ���P�����߶�AB�ϻ�������AB�ϣ����ݵȱ������ε����ʺ�ȫ�������ε������ҵ���ȹ�ϵ����������ת����������𰸣�
��3��������������з�������0��x��4ʱ���⣻��x��4ʱ�����ͼ�����������������Σ����PE�ij��ȣ��ú�x�Ĵ���ʽ��ʾ����PCQ����������ɸ�������ó�����x��һԪ���η��̣��ⷽ�̣���x��ֵ��
| 1 |
| 2 |
��2����Ϊ������������ǣ���P�����߶�AB�ϻ�������AB�ϣ����ݵȱ������ε����ʺ�ȫ�������ε������ҵ���ȹ�ϵ����������ת����������𰸣�
��3��������������з�������0��x��4ʱ���⣻��x��4ʱ�����ͼ�����������������Σ����PE�ij��ȣ��ú�x�Ĵ���ʽ��ʾ����PCQ����������ɸ�������ó�����x��һԪ���η��̣��ⷽ�̣���x��ֵ��
����⣺��1��֤��������PG��BC��AC��G��DH��AB��BQ��H��
�ߡ�ABC�DZ߳�Ϊ4�ĵȱ������Σ�
���DHC����APGΪ�ȱ������Σ�
��AP=CQ��
��PG=CQ����PGC=��DCQ=120�㣬
�ߡ�GPD=��Q��
�ߡ�PDG�ա�QDC��
��DP=DQ��
����ȷ����
��PE��AC��
��AE=EG��
��GD=DC��AB=BC=AC=4��
��GD+EG+AE+DC=4��
��2��GD+EG��=4��
��DE=2��
��2���١�PD=DQ��DH��AB��AP=x��CD=y��
��DH=
BP��
��AB=4��
��BP=4-x��BP=x-4��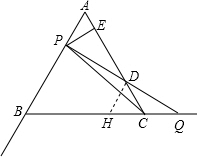
��y=
��4-x��=2-
x��0��x��4����y=
x-2��x��4����
�ڵ�0��x��4ʱ���⣬
��x��4ʱ��
��PE��AC����A=60��AP=x��
��PE=sin60���x=
x��
��AB=BC=AC=4��
��S��ABC=4
��
��PD=DQ��
����ͼ�ο�֪S��PCQ=2S��PDC=2��
��
��2��
=4
��
�ࣨ
x-2����
x=4
��
����ã�x2-4x-16=0��
��ã�x1=2-2
�����������⣬��ȥ�� x2=2+2
��
��x=2+2
��
�൱x=2+2
ʱ����PCQ��������ABC�������ȣ�
�ߡ�ABC�DZ߳�Ϊ4�ĵȱ������Σ�
���DHC����APGΪ�ȱ������Σ�
��AP=CQ��
��PG=CQ����PGC=��DCQ=120�㣬
�ߡ�GPD=��Q��
�ߡ�PDG�ա�QDC��
��DP=DQ��
����ȷ����
��PE��AC��
��AE=EG��
��GD=DC��AB=BC=AC=4��
��GD+EG+AE+DC=4��
��2��GD+EG��=4��
��DE=2��
��2���١�PD=DQ��DH��AB��AP=x��CD=y��
��DH=
| 1 |
| 2 |
��AB=4��
��BP=4-x��BP=x-4��

��y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�ڵ�0��x��4ʱ���⣬
��x��4ʱ��
��PE��AC����A=60��AP=x��
��PE=sin60���x=
| ||
| 2 |
��AB=BC=AC=4��
��S��ABC=4
| 3 |
��PD=DQ��
����ͼ�ο�֪S��PCQ=2S��PDC=2��
| y•PE |
| 2 |
��2��
| y•PE |
| 2 |
| 3 |
�ࣨ
| 1 |
| 2 |
| ||
| 2 |
| 3 |
����ã�x2-4x-16=0��
��ã�x1=2-2
| 5 |
| 5 |
��x=2+2
| 5 |
�൱x=2+2
| 5 |
������������Ҫ����ȱ������ε����ʡ�ȫ�������ε��ж������ʡ�����ʵ��������һ�κ�����ϵʽ�ȣ�����ؼ��������������ߣ��ҳ�������ϵ

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
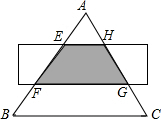 ��ͼ����ABC�DZ߳�Ϊ6cm�ĵȱ������Σ���һƽ����BC�ľ������أ�AB���س����ȷ֣���ͼ����Ӱ���ֵ����Ϊ��������
��ͼ����ABC�DZ߳�Ϊ6cm�ĵȱ������Σ���һƽ����BC�ľ������أ�AB���س����ȷ֣���ͼ����Ӱ���ֵ����Ϊ��������| A��4cm2 | ||
B��2
| ||
C��3
| ||
D��4
|
 y����������ཻ�ڵ�E����B��-1��0����P��AC�ϵ�һ�����㣨P���A��C���غϣ�
y����������ཻ�ڵ�E����B��-1��0����P��AC�ϵ�һ�����㣨P���A��C���غϣ� ��ͼ����ABC�DZ߳�Ϊ3�ĵȱ������Σ���BDC�ǵ��������Σ��ҡ�BDC=120�㣬��DΪ������һ��60��ǣ�ʹ�����߷ֱ�AB��M��AC�ڵ�N������MN�����AMN���ܳ�Ϊ��������
��ͼ����ABC�DZ߳�Ϊ3�ĵȱ������Σ���BDC�ǵ��������Σ��ҡ�BDC=120�㣬��DΪ������һ��60��ǣ�ʹ�����߷ֱ�AB��M��AC�ڵ�N������MN�����AMN���ܳ�Ϊ��������
