题目内容

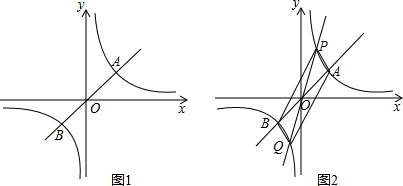
如图，△P1OA1、△P2A1A2是等腰直角三角形，点P1、P2在函数y=
4
x
(x＞0)的图象上，斜边OA1、A1A2都在x轴上，则点A2的坐标是（　　）
A．（2
2
-2，0）		B．（2
2
+2，0）		C．（4
2
，0）		D．（2
2
，0）

（1）根据等腰直角三角形的性质，可设点P1（a，a），
又y=
4
x
，
则a2=4，a=±2（负值舍去），
再根据等腰三角形的三线合一，得A1的坐标是（4，0），
设点P2的坐标是（4+b，b），又y=
4
x
，则b（4+b）=4，
即b2+4b-4=0，
又∵b＞0，∴b=2
2
-2，
再根据等腰三角形的三线合一，
∴4+2b=4+4
2
-4=4
2
，
∴点A2的坐标是（4
2
，0）．
故选C．
练习册系列答案
相关题目
在某一电路中，保持电压不变，电流I（安）与电阻R（欧）成反比例函数关系，其图象如图，则这一电路的电压为______伏．
某运输公司准备运输一批货物，需要的货船数量y（艘）与货船的核定装载量x（吨）之间的函数关系如图所示，请根据图象提供的信息回答问题：
（1）这批货物的质量是多少吨？
（2）写出y与x的函数关系式．
（3）如果要求出动货船不超过4艘，那么每艘货船的核定装载量至少要多少吨？
如图，直线y=-x+1与x轴交于点A，与y轴交于点B，P（a，b）为双曲线y=
1
2x
(x＞0)上的一点，PM⊥x轴于M，交AB于E，PN⊥y轴于N，交AB于F．
（1）当点P的坐标为（
3
4
，
2
3
）时，求E、F两点的坐标及△EOF的面积；
（2）用含a，b的代数式表示E、F两点的坐标及△EOF的面积；
（3）求BE•AF的值．
如图，正方形OAPB、等腰直角三角形ADF的顶点A，D，B在坐标轴上，点P，F在函数y=
9
x
(x＞0)的图象上，则点F的坐标为（　　）
A．(
3
5
-3
2
，
3
5
+3
2
)		B．(
8+2
7
2
，
8-2
7
2
)
C．(
3
5
+3
2
，
3
5
-3
2
)		D．(
8-2
7
2
，
8+2
7
2
)
某学校锅炉房建有一个储煤库，开学初购进一批煤，按每天用煤0.6吨计算，一学期（按150天计）刚好用完，若每天的耗煤量为x（吨），那么这批煤能维持y（天）．
（1）求y与x之间的函数关系式；
（2）在给定的坐标系中，作出（1）中求出的函数图象；
（3）若每天节约0.1吨煤，这批煤能维持多少天？
如图，矩形ABCD的对角线BD的中点经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=
k2+2k+1
x
的图象上．若点A的坐标为（-4，-1），则k的值为______．
三角形的面积为6cm2．
（1）求底边上的高ycm与底边xcm之间的函数关系式；
（2）作出这个函数的图象．
如图1，已知双曲线y=
k
x
(k＞0)与直线y=k′x交于A，B两点，点A在第一象限．试解答下列问题：
（1）若点A的坐标为（4，2），则点B的坐标为______；若点A的横坐标为m，则点B的坐标可表示为______；
（2）如图2，过原点O作另一条直线l，交双曲线y=
k
x
(k＞0)于P，Q两点，点P在第一象限．
①说明四边形APBQ一定是平行四边形；
②设点A，P的横坐标分别为m，n，四边形APBQ可能是矩形吗？可能是正方形吗？若可能，直接写出m，n应满足的条件；若不可能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网