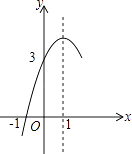题目内容
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.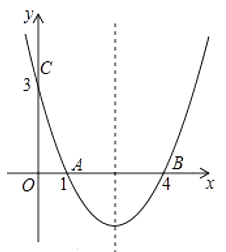
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
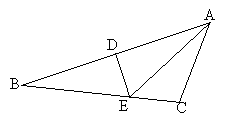
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
【答案】
(1)解:根据题意设抛物线的解析式为y=a(x﹣1)(x﹣4),
代入C(0,3)得3=4a,
解得a= ![]() ,
,
y= ![]() (x﹣1)(x﹣4)=
(x﹣1)(x﹣4)= ![]() x2﹣
x2﹣ ![]() x+3,
x+3,
所以,抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+3
x+3
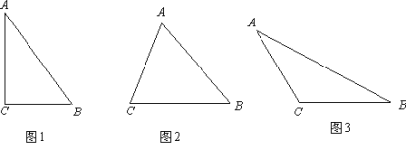
(2)解:∵A、B关于对称轴对称,如图1,连接BC,
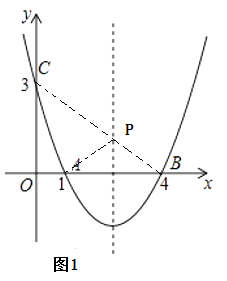
∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC= ![]() =5,
=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)解:∵B(4,0)、C(0,3),
∴直线BC的解析式为y=﹣ ![]() x+3,
x+3,
①当∠BQM=90°时,如图2,设M(a,b),
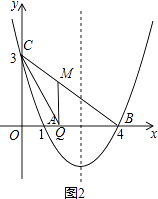
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得b=
,解得b= ![]() ,代入y=﹣
,代入y=﹣ ![]() x+3得,
x+3得, ![]() =﹣
=﹣ ![]() a+3,解得a=
a+3,解得a= ![]() ,
,
∴M( ![]() ,
, ![]() );
);
②当∠QMB=90°时,如图3,
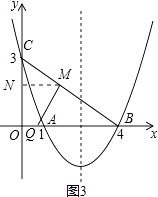
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴ ![]() =
= ![]() ,解得m=
,解得m= ![]() ,
,
作MN∥OB,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴MN= ![]() ,CN=
,CN= ![]() ,
,
∴ON=OC﹣CN=3﹣ ![]() =
= ![]() ,
,
∴M( ![]() ,
, ![]() ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)由抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点,用待定系数法求出解析式;(2)由A、B关于对称轴对称,得到BC与对称轴的交点即为所求的点P,由A(1,0)、B(4,0)、C(0,3),得到OA=1,OC=3,BC =5,OC+OA+BC=1+3+5=9;所以在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9;(3)由B(4,0)、C(0,3),所以直线BC的解析式为y=﹣ ![]() x+3,①当∠BQM=90°时,设M(a,b),由∠CMQ>90°,得到只能CM=MQ=b,因为MQ∥y轴,所以△MQB∽△COB,得到 比例,求出M的坐标;②当∠QMB=90°时,由∠CMQ=90°,得到只能CM=MQ,得到△BMQ∽△BOC,得到比例,解得m=
x+3,①当∠BQM=90°时,设M(a,b),由∠CMQ>90°,得到只能CM=MQ=b,因为MQ∥y轴,所以△MQB∽△COB,得到 比例,求出M的坐标;②当∠QMB=90°时,由∠CMQ=90°,得到只能CM=MQ,得到△BMQ∽△BOC,得到比例,解得m= ![]() ,由MN∥OB,得到比例,求出M(
,由MN∥OB,得到比例,求出M( ![]() ,
, ![]() ),在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(
),在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).

【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3个 | 4个 | 1200元 |
第二周 | 5个 | 3个 | 1450元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
(1)求A、B两种型号的足球的销售单价;
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个,求A种型号的足球最多能采购多少个?
(3)在![]() 的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.