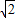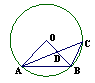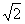题目内容
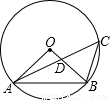
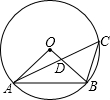 如图,⊙O的半径OB和弦AC相交于点D,∠AOB=90°,则下列结论错误的是( )
如图,⊙O的半径OB和弦AC相交于点D,∠AOB=90°,则下列结论错误的是( )| A、∠C=45° | ||
| B、∠OAB=45° | ||
C、OB:AB=1:
| ||
| D、∠ABC=4∠CAB |
分析:根据圆周角定理及等腰三角形的性质对各个选项进行分析,从而得到答案.
解答:解:∵∠AOB=90°,OA=OB
∴△AOB是等腰直角三角形
∴∠OAB=45°(B正确)
∴OB:AB=sin∠OAB=
=1:
(C正确)
∴∠C=
∠O=45°(A正确).
故选D.
∴△AOB是等腰直角三角形
∴∠OAB=45°(B正确)
∴OB:AB=sin∠OAB=
| ||
| 2 |
| 2 |
∴∠C=
| 1 |
| 2 |
故选D.
点评:本题利用了等腰直角三角形的判定和性质,正弦的概念及圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
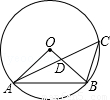
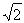
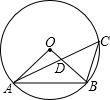 如图,⊙O的半径OB和弦AC相交于点D,∠AOB=90°,则下列结论错误的是
如图,⊙O的半径OB和弦AC相交于点D,∠AOB=90°,则下列结论错误的是