题目内容
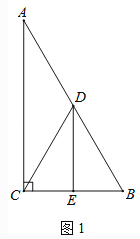
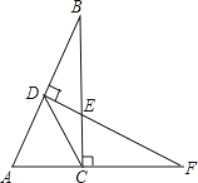
【题目】如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于E,交AC延长线于F.
求证:(1)△ADF∽△EDB;
(2)CD2=DEDF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据题意可得∠B+∠A=90°,∠A+∠F=90°,则∠B=∠F,从而得出△ADF∽△EDB;
(2)由(1)得∠B=∠F,再CD是Rt△ABC斜边AB上的中线,得出CD=DB,根据等边对等角得∠DCE=∠F,则可证明△CDE∽△FDC,从而得![]() ,化为乘积式即可CD2=DFDE.
,化为乘积式即可CD2=DFDE.
证明:(1)在Rt△ABC中,∠B+∠A=90°
∵DF⊥AB∴∠BDE=∠ADF=90°∴∠A+∠F=90°,
∴∠B=∠F,
∴△ADF∽△EDB;
(2)由(1)可知△ADF∽△EDB∴∠B=∠F,
∵CD是Rt△ABC斜边AB上的中线∴CD=AD=DB,∴∠DCE=∠B,∴∠DCE=∠F,
∴△CDE∽△FDC,∴![]() =
=![]() ,
,
∴CD2=DFDE.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?