题目内容
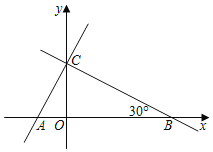
【题目】如图1,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于A,B两点,过点B在第二象限内作
轴分别交于A,B两点,过点B在第二象限内作![]() 且
且![]() ,连接
,连接![]() .
.
(1)求点C的坐标.
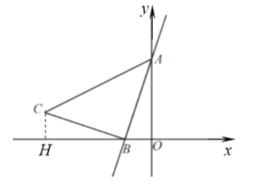
(2)如图2,过点C作直线![]() 轴交AB于点D,交
轴交AB于点D,交![]() 轴于点E,
轴于点E,
请从下列A,B两题中任选一题作答,我选择______题
A.①求线段CD的长.
②在坐标平面内,是否存在点M(除点B外),使得以点M,C,D为顶点的三角形与![]() 全等?若存在,请直接写出所有符合条件的点M的坐标:若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点M的坐标:若不存在,请说明理由.
B.①如图3,在图2的基础上,过点D作![]() 于点F,求线段DF的长.
于点F,求线段DF的长.
②在坐标平面内,是否存在点M(除点F外),使得以点M,C,D为顶点的三角形与![]() 全等?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.

【答案】(1)C(-4,1);(2)A:①![]() ;②
;②![]() ;B:①
;B:①![]() ;②
;②![]()
【解析】
(1)首先由直线解析式求得点A、B的坐标,再从点C向x轴作垂线,证明三角形全等,由此求得点C的坐标;(2)选择A时,①由![]() 轴,知点D的纵坐标,代入一次函数解析式即可求得横坐标,由此得到线段CD的长;②利用轴对称可得到点M的坐标;选择B时,①求出线段AC的长,再利用△ACD的面积就可求得DF的长度;②利用轴对称可得到点M的坐标
轴,知点D的纵坐标,代入一次函数解析式即可求得横坐标,由此得到线段CD的长;②利用轴对称可得到点M的坐标;选择B时,①求出线段AC的长,再利用△ACD的面积就可求得DF的长度;②利用轴对称可得到点M的坐标
解:(1)在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() 点A的坐标为(
点A的坐标为(![]()
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点B的坐标为![]() ,
,
![]()
过点C作![]() 轴于点H,则
轴于点H,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 点C在第二象限,
点C在第二象限,
![]() 点C的坐标为
点C的坐标为![]()
(2)A.①由(1)知点C的坐标为![]() ,
,
![]() 轴交AB于点D,
轴交AB于点D,![]() 点D的纵坐标为1,
点D的纵坐标为1,
将![]() 代入
代入![]() 得
得![]() ,
,
![]()
![]() 点D的坐标为
点D的坐标为![]() ,
,
![]()
②存在
当点M1与点B关于直线CD对称时,得点M1坐标为(-1,2);
当点M2与点B关于CD的垂直平分线对称时,得点M2坐标为![]() ;
;
当点M3与点点M2关于直线CD对称时,得点M3坐标为![]()
综上,当满足![]() 时,以点M,C,D为顶点的三角形与
时,以点M,C,D为顶点的三角形与![]() 全等
全等
B.①由(1)知点C的坐标为![]() ,
,
![]() 轴交AB于点D,交
轴交AB于点D,交![]() 轴于点E,
轴于点E,
![]() 点D的纵坐标为1,
点D的纵坐标为1,![]()
将![]() 代入
代入![]() 得
得![]()
![]() 点D的坐标为
点D的坐标为![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
由勾股定理得![]() ,
,
![]()
∴![]()
![]()
![]()
![]()
②存在
在Rt△CDF中,由勾股定理得![]()
∵![]()
∴![]()
即点F为线段AC靠近点A的一个三等分点,∴F(![]()
当点M1与点F关于直线CD对称时,点M1坐标为![]()
当点M2与点F关于线段CD的垂直平分线对称时,点M2坐标为![]() ;
;
当点M3与点F关于直线CD对称时,点M3坐标为![]()
综上,当满足![]() 时,以点M,C,D为顶点的三角形与
时,以点M,C,D为顶点的三角形与![]() 全等
全等

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案