Question

【题目】某数学活动小组在一次活动中，对一个数学问题作如下探究：

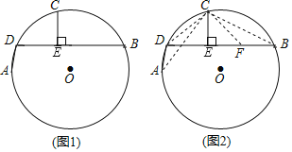
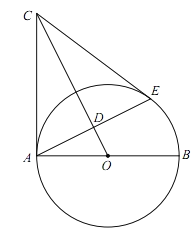
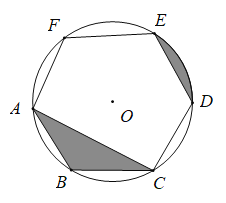
（问题发现）如图1，AD，BD为⊙O的两条弦（AD＜BD），点C为的中点，过C作CE⊥BD，垂足为E．求证：BE＝DE+AD．

（问题探究）小明同学的思路是：如图2，在BE上截取BF＝AD，连接CA，CB，CD，CF．……请你按照小明的思路完成上述问题的证明过程．

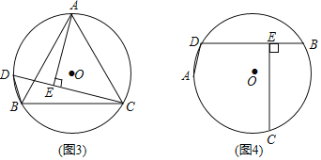
（结论运用）如图3，△ABC是⊙O的内接等边三角形，点D是上一点，∠ACD＝45°，连接BD，CD，过点A作AE⊥CD，垂足为E．若AB＝，则△BCD的周长为　 　．

（变式探究）如图4，若将（问题发现）中“点C为的中点”改为“点C为优弧的中点”，其他条件不变，上述结论“BE＝DE+AD”还成立吗？若成立，请说明理由；若不成立，请写出BE、AD、DE之间的新等量关系，并加以证明．

Answer 1

【答案】【问题发现】见解析；【问题探究】见解析；【结论运用】8+4；【变式探究】结论“BE＝DE+AD”不成立，BE+AD＝DE，理由见解析

【解析】

[问题探究]在BE上截取BF＝AD，连接CA，CB，CD，CF，证明△DAC≌△FBC，根据全等三角形的性质得到CD＝CF，根据等腰三角形的三线合一、结合图形证明结论；

[结论运用]连接AD，在CE上截取CF＝AD，连接AF，证明△DAB≌△FAC，得到DB+DC＝2EC，根据等腰直角三角形的性质求出EC，根据三角形的周长公式计算，得到答案；

[变式探究]在线段DE上截取DF＝AD，连接CB、CF、CD、CA，证明△ADC≌△FDC，根据全等三角形的性质、等腰三角形的性质解答即可．

解：[问题探究]如图2，在BE上截取BF＝AD，连接CA，CB，CD，CF，

∵点C为的中点，

∴＝，

∴AC＝BC，

由圆周角定理得，∠DAC＝∠DBC，

在△DAC和△FBC中，

，

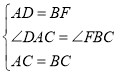∴△DAC≌△FBC（SAS）

∴CD＝CF，又CE⊥BD，

∴DE＝EF，

∴BE＝EF+BF＝DE+AD；

[结论运用]连接AD，在CE上截取CF＝AD，连接AF，

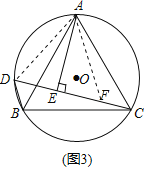
由[问题探究]可知，△DAB≌△FAC，

∴BD＝CF，AD＝AF，

∵AE⊥CD，

∴DE＝EF，

∴EC＝EF+CF＝DE+BD，

∴DB+DC＝2EC，

在Rt△AEC中，∠ACE＝45°，

∴EC＝AC＝4，

∴△BCD的周长＝DB+DC+BC＝8+4，

故答案为：8+4；

[变式探究]结论“BE＝DE+AD”不成立，BE+AD＝DE，

理由如下：在线段DE上截取DF＝AD，连接CB、CF、CD、CA，

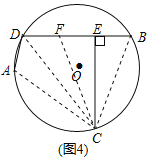
∵点C为优弧的中点”，

∴＝，

∴AC＝CB，∠ADC＝∠BDC，

在△ADC和△FDC中，

，

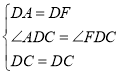∴△ADC≌△FDC（SAS），

∴CA＝CF，

∵CA＝CB，

∴CF＝CB，又CE⊥BD，

∴BE＝EF，

∴DE＝DF+EF＝BE+AD．