题目内容
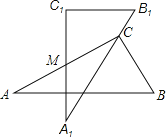
【题目】如图所示是两块完全一样的含30°角的三角板，分别记作△ABC和△A1B1C1，现将两块三角板重叠在一起，设较长直角边的中点为M，绕中点M转动三角板ABC，使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上，当∠A=30°，AC=10时，两直角顶点C，C1的距离是 ．
【答案】5
【解析】
试题分析：连接CC1，根据M是AC、A1C1的中点，AC=A1C1，得出CM=A1M=C1M=
AC=5，再根据∠A1=∠A1CM=30°，得出∠CMC1=60°，△MCC1为等边三角形，从而证出CC1=CM，即可得出答案．
解：如图，连接CC1，
∵两块三角板重叠在一起，较长直角边的中点为M，
∴M是AC、A1C1的中点，AC=A1C1，
∴CM=A1M=C1M=AC=5，
∴∠A1=∠A1CM=30°，
∴∠CMC1=60°，
∴△CMC1为等边三角形，
∴CC1=CM=5，
∴CC1长为5．
故答案为5．
练习册系列答案
相关题目
【题目】如果10b=n，那么称b为n的劳格数，记为b=d （n），由定义可知：10b=n与b=d （n）所表示的是b、n两个量之间的同一关系．
（1）根据劳格数的定义，填空：d（10）= ，d（10﹣2）= ；
劳格数有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（
）=d（m）﹣d（n）．
根据运算性质，填空：
= （a为正数）．
（2）下表中与数x对应的劳格数d （x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
d（x） | 3a﹣b+c | 2a﹣b | a+c | 1+a﹣b﹣c | 3﹣3a﹣3c | 4a﹣2b | 3﹣b﹣2c | 6a﹣3b |
