Question

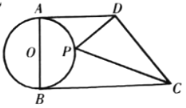
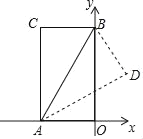
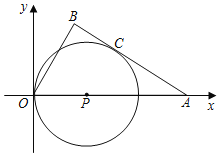
【题目】如图，在△ABO中，∠B=90 ，OB=3,OA=5，以AO上一点P为圆心，PO长为半径的圆恰好与AB相切于点C，则下列结论正确的是（　　）．

A.⊙P 的半径为

B.经过A，O，B三点的抛物线的函数表达式是

C.点（3，2）在经过A，O，B三点的抛物线上

D.经过A，O，C三点的抛物线的函数表达式是

Answer 1

【答案】D

【解析】

A、连接PC，根据已知条件可知△ACP∽△ABO，再由OP=PC，可列出相似比得出；

B、由射影定理及勾股定理可得点B坐标，由A、B、O三点坐标，可求出抛物线的函数表达式；

C、由射影定理及勾股定理可计算出点C坐标，将点C代入抛物线表达式即可判断；

D、由A，O，C三点坐标可求得经过A，O，C三点的抛物线的函数表达式．

解：如图所示，连接PC，

∵圆P与AB相切于点C，所以PC⊥AB，

又∵∠B=90，

所以△ACP∽△ABO，

设OP=x，则OP=PC=x，

又∵OB=3，OA=5，

∴AP=5-x，

∴，解得，

∴半径为，故A选项错误；

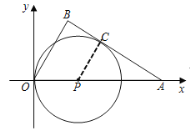
过B作BD⊥OA交OA于点D，

∵∠B=90，BD⊥OA，

由勾股定理可得：，

由面积相等可得：

∴，

∴由射影定理可得，

∴

∴，

设经过A，O，B三点的抛物线的函数表达式为；

将A(5,0)，O(0,0)，代入上式可得：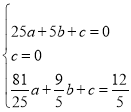

解得 ，，c=0,

经过A，O，B三点的抛物线的函数表达式为，

故B选项错误；

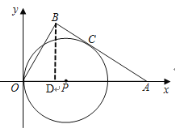
过点C作CE⊥OA交OA于点E，

∵，

∴由射影定理可知，

∴，所以，

由勾股定理得，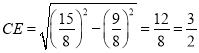

∴点C坐标为，

故选项C错误；

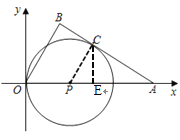
设经过A，O，C三点的抛物线的函数表达式是，

将A(5,0)，O(0,0)，代入得，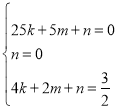

解得：，

∴经过A，O，C三点的抛物线的函数表达式是，

故选项D正确．