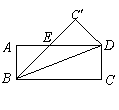
题目内容
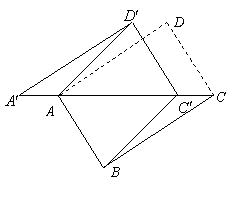
如图,将矩形![]() 沿对角线
沿对角线![]() 剪开,再把
剪开,再把![]() 沿
沿![]() 方向平移得到
方向平移得到![]() .
.
(1)证明![]() ;
;
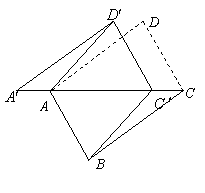 (2)若
(2)若![]() ,试问当点
,试问当点![]() 在线段
在线段![]() 上的什么位置时,四边形
上的什么位置时,四边形![]() 是菱形,并请说明理由.
是菱形,并请说明理由.
解:(1)证明:∵四边形ABCD是矩形,
△A′C′D′由△ACD平移得到,
∴A′D′=AD=CB,AA′=CC′,A′D′∥AD∥BC.
∴∠D′A′C′=∠BCA.
∴△A′AD′≌△CC![]() ′B.
′B.
(2)当点C′是线段AC的中点时,四边形ABC′D′是菱形.
理由如下:
∵四边形ABCD是矩形,△A′C′D′由△ACD平移得到,
∴C′D′=CD=AB.
由(1)知AD′=C′B.
∴四边形ABC′D′是平行四边形.
在Rt△ABC中,点C′是线段AC的中点,
∴BC′= ![]() AC.
AC.
而∠ACB=30°,
∴AB= ![]() AC.
AC.
∴AB=BC′.
∴四边形ABC′D′是菱形.

练习册系列答案
相关题目
 7、如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有( )
7、如图,将矩形纸片ABCD沿对角线BD折叠一次,则图中全等三角形有( )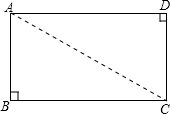 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4