��Ŀ����
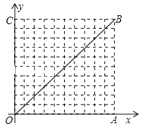
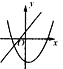
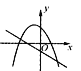
����Ŀ����֪��������l1��y=��x2+bx+3��x���ڵ�A��B������A�ڵ�B����ࣩ����y���ڵ�C����Գ���Ϊx=1��������l2������A����x�����һ������ΪE��5��0������y���ڵ�D��0���� ![]() ����
����
��1����������l2�ĺ�������ʽ��
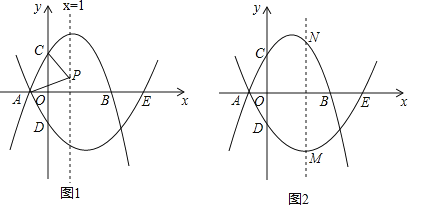
��2��PΪֱ��x=1��һ���㣬����PA��PC����PA=PCʱ�����P�����ꣻ
��3��MΪ������l2��һ���㣬����M��ֱ��MN��y�ᣬ��������l1�ڵ�N�����M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵ��
���𰸡���1��y=![]() x2��2x��
x2��2x��![]() ����2����1��1������3��12��
����2����1��1������3��12��
�������������������1���ɶԳ�������b�������l1�Ľ���ʽ����y=0�����A�����꣬�����ô���ϵ���������l2�ı���ʽ����2����P������Ϊ��1��y�����ɹ��ɶ����ɱ�ʾ��PC2��PA2���������ɵõ�����y�ķ��̿����y�������P�����ꣻ��3���ɷֱ����M��N�����꣬�ɱ�ʾ��MN���ٸ��ݺ��������ʿ����MN�����ֵ��
�����������1����������l1��y=��x2+bx+3�ĶԳ���Ϊx=1�� �ੁ![]() =1�����b=2��
=1�����b=2��
��������l1�Ľ���ʽΪy=��x2+2x+3�� ��y=0���ɵ���x2+2x+3=0�����x=��1��x=3��
��A����������1��0����
��������l2������A��E���㣬 ������������l2����ʽΪy=a��x+1����x��5����
����������l2��y���ڵ�D��0����![]() ���� �ੁ
���� �ੁ![]() =��5a�����a=
=��5a�����a=![]() �� ��y=
�� ��y=![]() ��x+1����x��5��=
��x+1����x��5��=![]() x2��2x��
x2��2x��![]() ��
��
��������l2�ĺ�������ʽΪy=![]() x2��2x��
x2��2x��![]() ��
��
��2����P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��PC2=12+��y��3��2=y2��6y+10��PA2=[1������1��]2+y2=y2+4�� ��PC=PA��
��y2��6y+10=y2+4�����y=1�� ��P��������1��1����
��3�����������M��x��![]() x2��2x��
x2��2x��![]() ���� ��MN��y�ᣬ ��N��x����x2+2x+3����
���� ��MN��y�ᣬ ��N��x����x2+2x+3����![]() x2��2x��
x2��2x��![]()
����x2+2x+3=![]() x2��2x��
x2��2x��![]() ���ɽ��x=��1��x=
���ɽ��x=��1��x=![]() ��
��
������1��x��![]() ʱ��MN=����x2+2x+3������
ʱ��MN=����x2+2x+3������![]() x2��2x��
x2��2x��![]() ��=��
��=��![]() x2+4x+
x2+4x+![]() =��
=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��Ȼ��1��![]() ��
��![]() ������x=
������x=![]() ʱ��MN�����ֵ
ʱ��MN�����ֵ![]() ��
��
����![]() ��x��5ʱ��MN=��
��x��5ʱ��MN=��![]() x2��2x��
x2��2x��![]() ��������x2+2x+3��=
��������x2+2x+3��=![]() x2��4x��
x2��4x��![]() =
=![]() ��x��
��x��![]() ��2��
��2��![]() ��
��
��Ȼ��x��![]() ʱ��MN��x�����������
ʱ��MN��x�����������
����x=5ʱ��MN�����ֵ��![]() ����5��
����5��![]() ��2��
��2��![]() =12��
=12��
���Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12��

����Ŀ�����꼶һ��������ͬѧ��һ����ѧ�����еijɼ�ͳ��������±���
�༶ | �μ����� | ��λ�� | ƽ���� | ���� |
һ | 49 | 84 | 80 | 186 |
�� | 49 | 85 | 80 | 161 |
ijͬѧ������õ����½��ۣ�
��һ�������ѧ��ƽ���ɼ���ͬ;
�ڶ���������������һ�ࣨ������85�֣�
��һ��ѧ���ijɼ�����ȶ���������ȷ���ǣ� ��
A. �٢� B. �٢� C. �٢ڢ� D. �ڢ�