Question

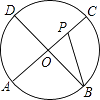
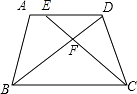
【题目】如图，△ABC为等腰直角三角形，∠ACB=90°，将△ABC绕点A逆时针旋转75°，得到△AB′C′，过点B′作B′D⊥CA，交CA的延长线于点D，若AC=4，则AD的长为（ ）

A.2
B.3
C.3
D.2

Answer 1

【答案】A
【解析】解：∵△ABC为等腰直角三角形，∠ACB=90°，∴∠CAB=∠B=45°，
∵AC=BC=4，
∴AB=4 ，
∵将△ABC绕点A逆时针旋转75°得到△AB′C′，
∴∠B′AB=75°，AB′=4 ，
∴∠DAB′=180°﹣75°﹣45°=60°，
∵B′D⊥CA，
∴∠DB′A=30°，
∴AD= AB′=2 ．
故选：A．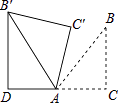

【考点精析】关于本题考查的等腰直角三角形和旋转的性质，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能得出正确答案．