题目内容
在直角三角形ABC中,∠C=90°,I是△ABC的三条内角平分线的交点,过I作ID⊥AB于D,若BD=m,AD=n,那么△ABC的面积为________.
mn
分析:I是内心,设内切圆半径为r,利用三角形的内切圆与内心的性质,S△ABC=(m+n)r+r2,再用勾股定理,将等式化简即可得出答案.
解答:I是内心,设内切圆半径为r,
2S△ABC=(m+n+m+r+n+r)r=2(m+n)r+2r2,
∴S△ABC=(m+n)r+r2,
三直角边长分别为m+n,m+r,n+r,
由勾股定理得到:(m+r)2+(n+r)2=(m+n)2,
∴(m+n)r+r2=mn,
∴S△ABC=mn.
故填:mn.
点评:此题主要考查学生对三角形面积,三角形内切圆与内心,勾股定理的理解和掌握,在计算中涉及到等式化简,这是此题的难点,也是此题的突破点.总之,此题属于难题.
分析:I是内心,设内切圆半径为r,利用三角形的内切圆与内心的性质,S△ABC=(m+n)r+r2,再用勾股定理,将等式化简即可得出答案.
解答:I是内心,设内切圆半径为r,
2S△ABC=(m+n+m+r+n+r)r=2(m+n)r+2r2,
∴S△ABC=(m+n)r+r2,
三直角边长分别为m+n,m+r,n+r,
由勾股定理得到:(m+r)2+(n+r)2=(m+n)2,
∴(m+n)r+r2=mn,
∴S△ABC=mn.
故填:mn.
点评:此题主要考查学生对三角形面积,三角形内切圆与内心,勾股定理的理解和掌握,在计算中涉及到等式化简,这是此题的难点,也是此题的突破点.总之,此题属于难题.

练习册系列答案
相关题目
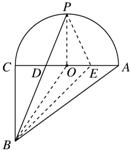 6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是
6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是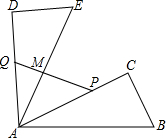 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.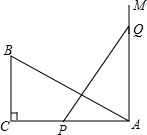 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?