题目内容
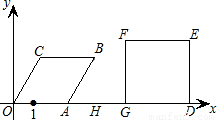
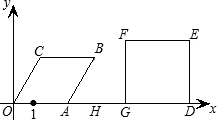
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点在x轴的上方作菱形OABC,且∠AOC=60°;同时点G从点D(8,0)出发,以2个单位长度/秒的速度沿x轴向负方向运动,以D、G为顶点在x轴的上方作正方形DEFG.设点A运动了t秒.求:(1)点B的坐标(用含t的代数式表示)
(2)当点A在运动的过程中,当t为何值时,点O、B、E在同一直线上;
(3)当点A在运动的过程中,是否存在t,使得以点C、G、D为顶点的三角形为等腰三角形?若存在
 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.
分析:(1)作BH⊥x轴于H点,根据OA=AB=t,表示出BH和AH的长即可求得B点的坐标;
(2)求得线段OB所在直线的解析式后将用t表示的E点的坐标代入就可以求得三点共线的时间t;
(3)用t表示出C、G点的坐标分①若CG=CD,则CG2=CD2、②若GC=GD,则GC2=GD2、③若DC=DG,则DC2=DG2三种情况求得存在的时间t.
(2)求得线段OB所在直线的解析式后将用t表示的E点的坐标代入就可以求得三点共线的时间t;
(3)用t表示出C、G点的坐标分①若CG=CD,则CG2=CD2、②若GC=GD,则GC2=GD2、③若DC=DG,则DC2=DG2三种情况求得存在的时间t.
解答:解:(1)作BH⊥x轴于H点,
∵OA=AB=1+t,∠AOC=∠BAH=60°
∴AH=
,BH=
(t+1),
∴OH=t+1+
=
,
∴B(
,
(t+1))(2分)
(2)将点B(
,
(t+1))代入直线OB的解析式y=kx,
解得直线的解析式为y=
x,
∵点E的坐标为(8,2t),且O、B、E三点共线,
∴∠BOD=30°
∴2t=
×8
解得:t=
(3分)
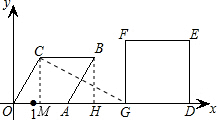
(3)过C作CM⊥x轴,交x轴于M,连接CG,
∵C(
,
),G(8-2t,0),D(8,0),
∴MG=OG-OM=8-2t-
,CM=
,
在直角三角形CMG中,CG2=MG2+CM2,
∴CG2=(
)2+
(1+t)2,
CD2=(
)2+
(1+t)2,GD2=4t2
假设存在满足条件的t,则
①若CG=CD,则CG2=CD2,
∴(
)2+
(1+t)2=(
)2+
(1+t)2t1=0(舍去)t2=5
②若GC=GD,则GC2=GD2
∴(
)2+
(1+t)2=4t2,t1=6+
,t2=6-
,
③若DC=DG,则DC2=DG2
∴(
)2+
(1+t)2=4t2,t1=-1+2
,t2=-1-2
(舍去)(11分)(每种情况2分)
∴存在满足条件的t值为:5,6+
,6-
,-1+2
(12分)
∵OA=AB=1+t,∠AOC=∠BAH=60°
∴AH=
| 1+t |
| 2 |
| ||
| 2 |
∴OH=t+1+
| t+1 |
| 2 |
| 3t+3 |
| 2 |
∴B(
| 3t+3 |
| 2 |
| ||
| 2 |
(2)将点B(
| 3t+3 |
| 2 |
| ||
| 2 |
解得直线的解析式为y=
| ||
| 3 |
∵点E的坐标为(8,2t),且O、B、E三点共线,
∴∠BOD=30°
∴2t=
| ||
| 3 |
解得:t=
| 4 |
| 3 |
| 3 |

(3)过C作CM⊥x轴,交x轴于M,连接CG,
∵C(
| 1+t |
| 2 |
| ||||
| 2 |
∴MG=OG-OM=8-2t-
| 1+t |
| 2 |
| ||||
| 2 |
在直角三角形CMG中,CG2=MG2+CM2,
∴CG2=(
| 15-5t |
| 2 |
| 3 |
| 4 |
CD2=(
| 15-t |
| 2 |
| 3 |
| 4 |
假设存在满足条件的t,则
①若CG=CD,则CG2=CD2,
∴(
| 15-5t |
| 2 |
| 3 |
| 4 |
| 15-t |
| 2 |
| 3 |
| 4 |
②若GC=GD,则GC2=GD2
∴(
| 15-5t |
| 2 |
| 3 |
| 4 |
| 17 |
| 17 |
③若DC=DG,则DC2=DG2
∴(
| 15-t |
| 2 |
| 3 |
| 4 |
| 5 |
| 5 |
∴存在满足条件的t值为:5,6+
| 17 |
| 17 |
| 5 |
点评:本题考查了相似三角形的判定及性质、等腰三角形、勾股定理等知识,是一道综合性较强的题目,特别是题目中涉及到的动点问题,更是中考的一个高频考点.

练习册系列答案
相关题目
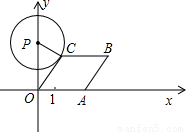
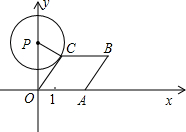 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求: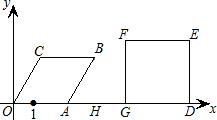 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.