题目内容
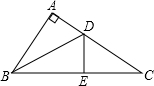
如图，已知在△ABC中，AB=AC，∠A=120°，AB的垂直平分线MN分别交BC、AB于点M、N，若BM=2cm，则CM=（ ）
| A．2cm | B．3cm | C．4cm | D．5cm |
如图，连接AM，
∵AB=AC，∠A=120°，
∴∠B=∠C=
（180°-120°）=30°，
∵MN是线段AB的垂直平分线，
∴AM=BM=2cm，
∴∠BAM=∠B=30°，
∠CAM=∠BAC-∠BAM=120°-30°=90°，
在Rt△ACM中，CM=2AM=2×2=4cm．
故选C．
∵AB=AC，∠A=120°，
∴∠B=∠C=
| 1 |
| 2 |
∵MN是线段AB的垂直平分线，
∴AM=BM=2cm，
∴∠BAM=∠B=30°，
∠CAM=∠BAC-∠BAM=120°-30°=90°，
在Rt△ACM中，CM=2AM=2×2=4cm．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
