题目内容
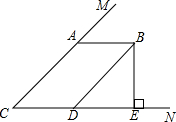如图，∠MCN=45°，且AB∥CD，AC∥BD，BE上CN于点E，求∠DBE的度数．
解：∵AC∥BD，
∴∠BDE=∠MCN=45°，
又∵BE⊥CE，
∴∠DEB=90°，
则∠DBE=90°-∠DEB=90°-45°=45°．
分析：根据AC∥BD，可得出∠BDE=∠MCN=45°，然后根据BE⊥CN求得∠DBE的度数．
点评：本题考查了平行线的性质，解答本题的关键是熟练掌握平行线的性质：两直线平行，同位角相等．
∴∠BDE=∠MCN=45°，
又∵BE⊥CE，
∴∠DEB=90°，
则∠DBE=90°-∠DEB=90°-45°=45°．
分析：根据AC∥BD，可得出∠BDE=∠MCN=45°，然后根据BE⊥CN求得∠DBE的度数．
点评：本题考查了平行线的性质，解答本题的关键是熟练掌握平行线的性质：两直线平行，同位角相等．
练习册系列答案
阅读快车系列答案
相关题目
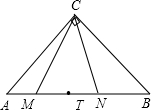如图，在等腰Rt△ABC中，∠ACB=90°，CA=CB，点M、N是AB上任意两点，且∠MCN=45°，点T为AB的中点．以下结论：①AB=
已知：如图，正方形ABCD的边长为a，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN．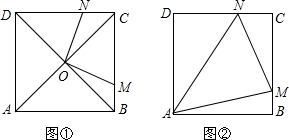
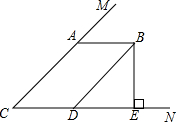如图，∠MCN=45°，且AB∥CD，AC∥BD，BE上CN于点E，求∠DBE的度数．