Question

【题目】如图，在△ABC中，AB=8，AC=4，G为BC的中点，DG⊥BC交∠BAC的平分线AD于D，DE⊥AB于E，DF⊥AC于F交AC的延长线于F．

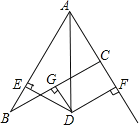
（1）求证：BE=CF；

（2）求AE的长．

Answer 1

【答案】（1）见解析；（2）6

【解析】

试题分析：（1）连接DB、DC，先由角平分线的性质就可以得出DE=DF，再证明△DBE≌△DCF就可以得出结论；

（2）由条件可以得出△ADE≌△ADF，就可以得出AE=AF，进而就可以求出结论．

解：（1）如图，连接DB、DC，

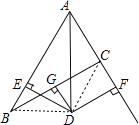
∵DG⊥BC且平分BC，

∴DB=DC．

∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，

∴DE=DF．∠AED=∠BED=∠ACD=∠DCF=90°

在Rt△DBE和Rt△DCF中

Rt△DBE≌Rt△DCF（HL），

∴BE=CF．

（2）在Rt△ADE和Rt△ADF中

∴Rt△ADE≌Rt△ADF（HL）．

∴AE=AF．

∵AC+CF=AF，

∴AE=AC+CF．

∵AE=AB﹣BE，

∴AC+CF=AB﹣BE

∵AB=8，AC=4，

∴4+BE=8﹣BE，

∴BE=2，

∴AE=8﹣2=6．