Question

【题目】如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE．F为AE上一点，且∠BFE=∠C．

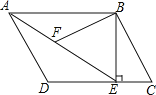
（1）求证：△ABF∽△EAD；

（2）若AB=4，BE=3，AD=，求BF的长．

Answer 1

【答案】（1）证明见解析；（2）BF=．

【解析】

试题分析：（1）求三角形相似就要得出两组对应的角相等，已知了∠BFE=∠C，根据等角的补角相等可得出∠ADE=∠AFB，根据AB∥CD可得出∠BAF=∠AED，这样就构成了两三角形相似的条件．

（2）根据（1）的相似三角形可得出关于AB，AE，AD，BF的比例关系，有了AD，AB的长，只需求出AE的长即可．可在直角三角形ABE中用勾股定理求出AE的长，这样就能求出BF的长了．

（1）证明：在平行四边形ABCD中，

∵∠D+∠C=180°，AB∥CD，

∴∠BAF=∠AED．

∵∠AFB+∠BFE=180°，∠D+∠C=180°，∠BFE=∠C，

∴∠AFB=∠D，

∴△ABF∽△EAD．

（2）解：∵BE⊥CD，AB∥CD，

∴BE⊥AB．

∴∠ABE=90°．

∴AE===5．

∵△ABF∽△EAD，

∴=，

∴=．

∴BF=．