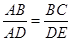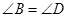题目内容
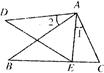
如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
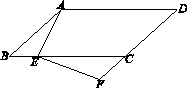
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长.

(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长.
(1)欲求△ABE∽△ECF ,由已知得到两三角形两个对应角相等,所以,两三角行相似(2)FC=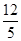
试题分析:由题意根据平行四边形的性质,可得到两个三角形的对应角相等,∴△ABE∽△ECF,再由相似比,得到所求的值。(1)证明:如图.
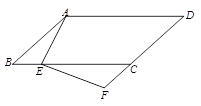
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠B=∠ECF,∠DAE=∠AEB.……2分
又∵∠DAE=∠F,
∴∠AEB=∠F.
∴△ABE∽△ECF. ........................................................ 3分
(2)解:∵△ABE∽△ECF,
∴
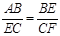 . ............................................................ 4分
. ............................................................ 4分∵四边形ABCD是平行四边形,
∴BC=AD=8.
∴EC=BC
 BE=8
BE=8 2="6."
2="6." ∴
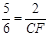 .
.∴
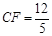 . ……………………………………………5分
. ……………………………………………5分点评:由平行四边形的性质得到对边平行,从而知角的相等,根据等量代换,由已知得到角相等,相似三角形两角相等即相似。两三角形相似对应边成比例,由已知列方程求之。本题属于基础题型。

练习册系列答案
相关题目
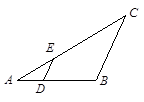
 中,D是AC上一点,E是AB上一点,且∠AED =∠C.
中,D是AC上一点,E是AB上一点,且∠AED =∠C.
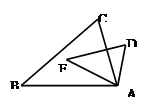
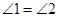 ,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )
,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )