题目内容
(1)如图,直线l 、l
、l 分别与直线l
分别与直线l 、l
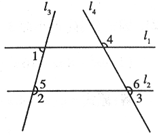
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.

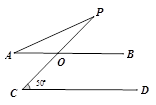
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.

 、l
、l 分别与直线l
分别与直线l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.

(1)112°;(2)∠AED=∠ACB
试题分析:(1)如图所示,由∠2+∠5=180°,∠2=104°,可求得∠5=76°,即可得到∠1=∠5,从而可以证得l
 ∥l
∥l ,根据平行线的性质可得∠4=∠6,再结合∠3=68°,∠3+∠6=180°求解;
,根据平行线的性质可得∠4=∠6,再结合∠3=68°,∠3+∠6=180°求解;(2)先根据同角的补角相等可得∠2=∠EFD,即可证得AB∥EF,根据平行线的性质可得∠3=∠ADE,由∠3=∠B可得∠B=∠ADE,即可证得DE∥BC,从而可以求得结果.
解:(1)如图:
∵∠2+∠5=180°,∠2=104°,
∴∠5=76°.
∵∠1=76°.
∴∠1=∠5.
∴l
 ∥l
∥l
∴∠4=∠6.
∵∠3=68°,∠3+∠6=180°,
∴∠6=112°.
∴∠4=112°;
(2)∠AED=∠ACB
∵∠1+∠EFD=180°,∠1+∠2=180°
∴∠2=∠EFD
∴AB∥EF
∴∠3=∠ADE
∵∠3=∠B
∴∠B=∠ADE
∴DE∥BC
∴∠AED=∠ACB.
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目