题目内容
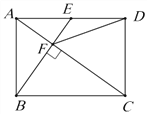
【题目】如图,已知矩形ABCD,用直尺和圆规进行如下操作:
①以点A为圆心,以AD的长为半径画弧交BC于点E;
②连接AE,DE;
③作DF⊥AE于点F.
根据操作解答下列问题:
(1)线段DF与AB的数量关系是 .
(2)若∠ADF=60°,求∠CDE的度数.

【答案】(1)DF=AB;(2)15°
【解析】
(1)利用角平分线的性质定理证明DF=DC即可解决问题;
(2)只要证明∠EDCC=∠EDF即可;
解:(1)结论:DF=AB.
理由:∵四边形ABCD是矩形,
∴AB=CD,AD∥BC,∠C=90°,
∵AD=AE,
∴∠ADE=∠AED=∠DEC,
∵DF⊥AE,DC⊥BC,
∴DF=DC=AB.
故答案为DF=AB.
(2)∵DE=DE,DF=DC,
∴Rt△DEF≌△DEC,
∴∠EDF=∠EDC,
∵∠ADF=60°,∠ADC=90°,
∴∠CDF=30°,
∴∠CDE=![]() ∠CDF=15°.
∠CDF=15°.


练习册系列答案
相关题目