题目内容
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
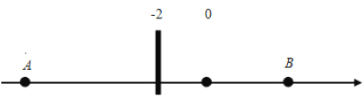
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
【答案】(1)16 (2)16 (3)2或14 (4)甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.
【解析】
(1)根据数轴上两点之间的距离公式计算即可;
(2)先根据P点在数轴上的位置分类讨论,然后求最小值即可;
(3)由题意可知:点C距离B点较近,设点C所表示的数为y,然后根据点C与点B的位置分类讨论即可;
(4)根据题意:点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
解:(1)![]()
故答案为:16;
(2)根据数轴上两点的距离公式可知:![]() 表示点P与点A之间的距离,
表示点P与点A之间的距离,![]() 表示点P与点B之间的距离
表示点P与点B之间的距离
①若点P在A点左侧时,即x<﹣10,由下图可知:PB>AB=16,即![]()
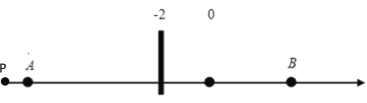
∴此时![]() ;
;
②若点P在线段AB上时,即﹣10≤x≤6,由下图可知:PA+PB=AB=16,
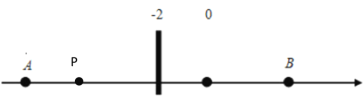
∴此时![]() ;
;
③若点P在B点右侧时,即x>6,由下图可知:PA>AB=16,即![]()
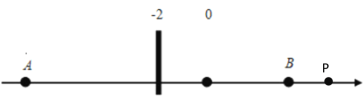
∴此时![]() ;
;
综上所述:![]() (当点P在线段AB上时,即﹣10≤x≤6,取等号)
(当点P在线段AB上时,即﹣10≤x≤6,取等号)
∴![]() 的最小值是16;
的最小值是16;
故答案为:16.
(3)∵![]()
∴点C距离B点较近
设点C所表示的数为y
①当C在B点左侧时,如下图所示,
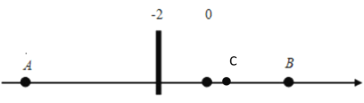
∴AC=y-(﹣10)=y+10,BC=6-y
∵![]()
∴y+10=3(6-y)
解得:y=2;
②当C在B点右侧时,如下图所示,
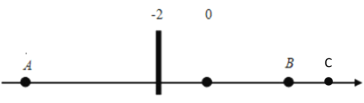
∴AC=y-(﹣10)=y+10,BC= y -6
∵![]()
∴y+10=3(y -6)
解得:y=14.
综上所述:![]() 点表示的数是2或14.
点表示的数是2或14.
(4)点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,
s,乙球从B到﹣2所需时间为:8÷2=4s,
∴运动![]() 秒钟后,甲球表示的数是:
秒钟后,甲球表示的数是:![]() 或
或![]() ;
;
乙球表示的数是:![]() 或
或![]() ,
,
∴![]() 或
或![]() ,或
,或![]() .
.
∴甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】用火柴按下图中的方式搭图形:

(1)按图示规律补全表格:
图形编号 | ① | ② | ③ | ④ | ⑤ |
火柴棒根数 | 7 | 12 |
|
|
|
(2)按照这种方式搭下去,请写出搭第n个图形需要的火柴根数;
(3)小明发现:按照这种方式搭图形会产生若干个正方形,若使用187根火柴搭图形,图中会产生多少个正方形?
【题目】某种水果的价格如表:
购买的质量(千克) | 不超过10千克 | 超过10千克 |
每千克价格 | 6元 | 5元 |
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?