题目内容
【题目】已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到Q、C两点重合时(如图①),求AP的长;
(2)点P运动过程中,有几个位置(几种情况)使△CQD的面积为![]() (直接写出答案)?
(直接写出答案)?
(3)当使△CQD的面积为![]() ,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.
,且Q位于以CD为直径的半圆上,CQ>QD时(如图②),求AP的长.

【答案】(1)AP=![]() ;(2)有4个位置;(3)AP=
;(2)有4个位置;(3)AP=![]() .
.
【解析】试题分析:本小问是利用切线的性质,得到∠ACP=90°,CD=2,得到半径的长度:OD=OC=OB,从而利用解直角三角形的方法来解得AP的长度;利用三角形的面积公式,知底和积可求高,然后用平行线去截圆,即可以得到解;利用S△CQD=![]() ,求出CD上的高QN的长度,过点PM⊥AD于点M,然后利用相似△QCN∽△DQN求出CN的长度,再次利用相似△PMC∽△QNC,从而得到MC与MP的关系,由已知易知AM=
,求出CD上的高QN的长度,过点PM⊥AD于点M,然后利用相似△QCN∽△DQN求出CN的长度,再次利用相似△PMC∽△QNC,从而得到MC与MP的关系,由已知易知AM=![]() ,由AC=1,从而可以解出MP,从而求出AP的长度.
,由AC=1,从而可以解出MP,从而求出AP的长度.
试题解析:(1)、∵AB是圆O的切线 ∴∠OBA=90°
∵![]() ABC中,CD=2,∠DAB=30° ∴OB=1 ∴OB=OC=AC=1
ABC中,CD=2,∠DAB=30° ∴OB=1 ∴OB=OC=AC=1
∵当点P,运动到Q、C两点重合时 ∴PC为圆O的切线 ∴∠PCA=90°
∵∠DAB=30°,AC=1 ∴AP=![]()
(2)、由于CD的长度2,而S△CQD=![]() ,故CD上的高的长度为:
,故CD上的高的长度为:![]() ,从而如图,我们可得到答案:
,从而如图,我们可得到答案:
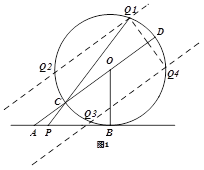
(3)、过点Q作QN⊥AD于点N, 过点P作PM⊥AD于点M ∵S△CQD=![]()
∴![]() QN×CD=
QN×CD=![]() ∴CD=
∴CD=![]() ∵CD是圆O的直径 ∴∠CQD=90°
∵CD是圆O的直径 ∴∠CQD=90°
易证△QCN∽△DQN ∴![]() ∴
∴![]()
设CN=X,则DN=2-x ∴![]() 解得:
解得:![]()
∵CQ>QD ∴CN=![]() ∴
∴![]()
易证:PMC∽△QNC 易得:![]() ∴
∴![]()
在![]() AMP中易得:
AMP中易得:![]() ∵AM+CM=AC=1
∵AM+CM=AC=1
∴![]() +
+![]() =1 ∴MP=
=1 ∴MP=![]() ∴AP=2MP=
∴AP=2MP=![]()



