题目内容
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线顶点为
,抛物线顶点为![]() ,下列四个结论:①无论
,下列四个结论:①无论![]() 取何值,
取何值,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 是等腰直角三角形;③若
是等腰直角三角形;③若![]() 则
则![]() ;④抛物线上有两点
;④抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论是( )
.其中正确的结论是( )
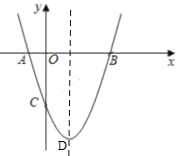
A.①②④B.②③④C.①②D.①③
【答案】A
【解析】
根据抛物线解析式可知C(0,t),把解析式配方可得顶点D(1,t-1),根据两点间距离公式可对①进行判断;当t=0时,根据抛物线解析式可得A、B、D三点坐标,利用两点间距离公式求出AD、BD、AB的长,根据勾股定理逆定理即可对②进行判定;根据抛物线解析式可得对称轴为直线x=1,根据二次函数的对称性即可对③进行判定;由![]() 可得x1-1>1-x2,根据x1、x2的取值范围可比较两点与对称轴的距离的远近,根据二次函数的性质可对④进行判定;综上即可得答案.
可得x1-1>1-x2,根据x1、x2的取值范围可比较两点与对称轴的距离的远近,根据二次函数的性质可对④进行判定;综上即可得答案.
∵![]() =(x-1)2+t-1,
=(x-1)2+t-1,
∴顶点D坐标为(1,t-1),对称轴为直线x=1,
当x=0时,y=t,
∴点C坐标为(0,t),
∴CD=![]() =
=![]() ,
,
∴无论![]() 取何值,
取何值,![]() 恒成立,故①正确,
恒成立,故①正确,
当t=0时,方程为y=x2-2x,顶点D坐标为(1,-1),
令y=0,则x2-2x=0,
解得:x1=0,x2=2,
∴A(0,0),B(2,0),
∵A、B关于对称轴x=1对称,
∴△ABD是等腰三角形,AD=BD=![]() =
=![]() ,AB=2,
,AB=2,
∵(![]() )2+(
)2+(![]() )2=22,
)2=22,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,
∴△ABD是等腰直角三角形,故②正确,
∵A(a,0),B(b,0)根据对称轴x=1对称,
∴当a=-1时,b=3,故③错误,
∵![]() ,
,
∴x1-1>1-x2,
∵![]() ,
,
∴x1-1<0,1-x2<0,
∴|x1-1|<|1-x2|,
∴点M到对称轴的距离小于点N到对称轴的距离,
∵1>0,
∴抛物线的开口向上,
∴y1<y2,故④正确,
综上所述:正确的结论有①②④,
故选:A.

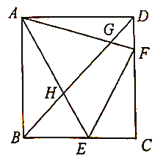
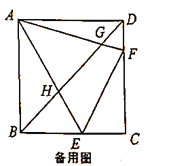
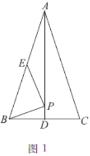
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() .在线段
.在线段![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,设
,设![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为0),
的值为0),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变换而变化的规律进行了探究.
的变换而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
(说明:补全表格时,相关数值保留一位小数)
(参考数据:![]() ,
,![]() ,
,![]() )
)
(2)建立平面直角坐标系(图2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)函数![]() 的最小值为 (保留一位小数),此时点
的最小值为 (保留一位小数),此时点![]() 在图1中的什么位置.
在图1中的什么位置.

【题目】为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |

(1)填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)将频数分布直方图补充完整;
(3)该校对成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为![]() ,请你估算全校获得二等奖的学生人数;
,请你估算全校获得二等奖的学生人数;
(4)结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.
【题目】2020年2月9日起,受新冠疫情影响,重庆市所有中小学实行“线上教学”,落实教育部“停课不停学”精神.某重点中学初![]() 级为了落实教学常规,特别要求家校联动,共同保证年级
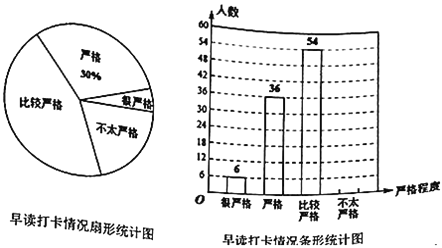
级为了落实教学常规,特别要求家校联动,共同保证年级![]() 名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
名学生上网课期间的学习不受太大影响.为了了解家长配合情况,年级对家长在“钉钉”上早读打卡的严格程度进行了调查,调查结果分为“很严格”,“严格”,“比较严格”和“不太严格”四类.年级抽查了部分家长的调查结果,绘制成如图所示的扇形统计图和条形统计图.
接着,年级对早读打卡“不太严格”的全体学生进行了第一次基础知识检测,同时召开专题家长会提醒,督促这些家长落实责任,并告知将再次进行检测.两周后,年级又对之前早读打卡“不太严格”的这部分学生进行了第二次基础知识检测.
[整理、描述数据]
以下是抽查的家长打卡“不太严格”的对应学生的两次检测(满分均为![]() 分)情况:
分)情况:
分数段 |
|
|
|
|
|
第一次人数 |
|
|
|
|
|
第二次人数 |
|
|
|
|
|
[分析数据]:
众数 | 中位数 | 平均数 | |
第一次 |
|
|
|
第二次 |
|
|
|
请根据调查的信息
(1)本次参与调查的学生总人数是___,并补全条形统计图;
(2)计算![]() ____,
____,![]() ____,并请你估计全年级所有被检测学生中,第二次检测得分不低于
____,并请你估计全年级所有被检测学生中,第二次检测得分不低于![]() 分的人数;
分的人数;
(3)根据调查的相关数据,请选择适当的统计量评价学校对早读打卡“不太严格”的家长召开专题家长会的效果.