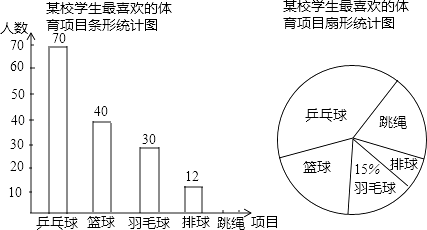
题目内容
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
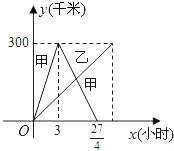
【答案】(1)y=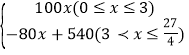 ;(2)出发后
;(2)出发后![]() 小时,两车离各自出发地的距离相等;(3)两车第一次相遇时间为第
小时,两车离各自出发地的距离相等;(3)两车第一次相遇时间为第![]() 小时,第二次相遇时间为第6小时.
小时,第二次相遇时间为第6小时.
【解析】
(1)由图知,该函数关系在不同的时间里表现成不同的关系,需分段表达.当行驶时间小于3时是正比例函数;当行使时间大于3小时小于![]() 小时是一次函数.可根据待定系数法列方程,求函数关系式.
小时是一次函数.可根据待定系数法列方程,求函数关系式.
(2)设出发后a小时,两车离各自出发地的距离相等,列出方程即可解决问题;
(3)两者相向而行,相遇时甲、乙两车行使的距离之和为300千米,列出方程解答,由题意有两次相遇.
(1)当0≤x≤3时,是正比例函数,设为y=kx,
x=3时,y=300,代入解得k=100,所以y=100x;
当3<x≤![]() 时,是一次函数,设为y=kx+b,
时,是一次函数,设为y=kx+b,
代入两点(3,300)、(![]() ,0),得
,0),得![]() 解得
解得![]() ,
,
所以y=540﹣80x.
综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式 为:y=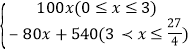 ;
;
(2)设出发后a小时,两车离各自出发地的距离相等.
由题意﹣80a+540=40a,
解得a=![]() s,
s,
答:出发后![]() 小时,两车离各自出发地的距离相等.
小时,两车离各自出发地的距离相等.
(3)由题意有两次相遇.
①当0≤x≤3,100x+40x=300,解得x=![]() ;
;
②当3<x≤![]() 时,(540﹣80x)+40x=300,解得x=6.
时,(540﹣80x)+40x=300,解得x=6.
综上所述,两车第一次相遇时间为第![]() 小时,第二次相遇时间为第6小时.
小时,第二次相遇时间为第6小时.

 阅读快车系列答案
阅读快车系列答案【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分) | |
八年1班 | 80 86 88 80 88 99 80 74 91 89 |
八年2班 | 85 85 87 97 85 76 88 77 87 88 |
八年3班 | 82 80 78 78 81 96 97 87 92 84 |
解答下列问题:
(1)请填写下表:
平均数(分) | 众数(分) | 中位数(分) | |
八年1班 | 85.5 |
| 87 |
八年2班 | 85.5 | 85 |
|
八年3班 |
| 78 | 83 |
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.