题目内容
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)
【答案】①③④
【解析】解:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2 ,
即42+x2=(8﹣x)2 ,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,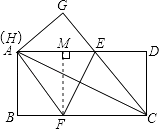
则ME=(8﹣3)﹣3=2,
由勾股定理得,
EF= ![]() =
= ![]() =2
=2 ![]() ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个,
故答案为①③④.
①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;③点H与点A重合时,设BF=x,表示出AF=FC=8﹣x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】旭日商场销售A,B两种品牌的钢琴,这两种钢琴的进价和售价如下表所示:
A | B | |
进价(万元/.套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种钢琴若干套,共需66万元,全部销售后可获毛利润9万元.(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进A,B两种品牌的钢琴各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种钢琴的购进数量,增加B种钢琴的购进数量,已知B种钢琴增加的数量是A种钢琴减少数量的1.5倍,若用于购进这两种钢琴的总资金不超过69万元,问A种钢琴购进数量至多或减少多少套?






